新薬の効果検証や治療法の比較など、医学研究の分野において最も信頼性の高いエビデンスとされるのが、被験者をランダムに割り付けるランダム化比較試験(RCT)です。しかしながら、被験者の背景をランダムに割り付ける、ということは、倫理的な問題やコスト、実務上の制約により難しいため、RCT以外の臨床試験も広く行われています。研究者によって条件操作を行わない観察データを用いた、観察研究が重要な役割を果たしています(参考文献1)。
本サイトでは、こうした観察研究において複数の変数の影響を調整する方法として、重回帰分析やロジスティック回帰分析を紹介してきました。


重回帰分析は、他の変数の影響を数式上で調整(制御)する手法です。しかし、あくまで「数式モデルによる補正」を行うものであるため、「本当に比較可能な人たち同士を適切に比較できているのか?」という、データの質の担保(共変量のバランス)を直感的に確認しにくいという側面があります。単に数式に当てはめるだけでは、実態とかけ離れた補正をしてしまっているリスクもあります。
そこで今回紹介するのが、観察データからあたかもランダムな割付のような比較可能なペアを作り出し、因果関係に迫るための手法、傾向スコア・マッチング(Propensity Score Matching)です。これにより、背景属性(共変量)のバランスを整え、より妥当性の高い効果検証を行うことができます。
現在では医学分野をはじめ、経済学・マーケティングなどの分野でも必須の統計手法として幅広く利用されています。
1. 傾向スコア分析とは?
2. 傾向スコア・マッチング
3. 使用するパッケージとデータの前処理
4. 傾向スコアの推定とマッチング
5. バランスの評価(適合度の確認)
6. 効果の推定と可視化
7. まとめ
1. 傾向スコア分析とは?
傾向スコア分析は、様々な共変量(年齢、性別、既往歴など)の情報を、「ある処置(介入)を受ける確率(予測確率)」という1つのスコア(傾向スコア)に要約し、そのスコアを用いて群間の比較を行う統計手法です。 主なアプローチとして以下の方法があります。
・傾向スコア・マッチング(Matching): スコアが似た人同士をペアにして、疑似的なRCT集団を作る。
・IPW(Inverse Probability Weighting):スコアの逆数で重み付けをして、集団全体のバランスを整えて、疑似的なRCT集団を作る。
2. 傾向スコア・マッチング
今回紹介する傾向スコア・マッチングでは、マッチングの良さを示す指標(標準化平均差:SMDなど)を通じて、統計的に共変量のバランスが取れているか検証できます。
| 項目 | 通常の重回帰分析 | 傾向スコア・マッチング |
|---|---|---|
| アプローチ | 共変量をモデル式に投入して調整 | 共変量のバランスを整えて疑似RCTを作成 |
| モデルの仮定 | 結果と共変量の線形関係などを仮定 | モデルへの依存度が比較的低い |
| 比較可能性 | 分布が大きく異なると補正困難 | 似た対象者のみを比較するため解釈しやすい |
| 可視化 | 散布図や回帰直線 | Love Plotによってバランス改善を視覚化 |
3. 使用パッケージとデータの前処理
◆使用パッケージ
library(MASS) # birthwtデータが含まれるパッケージ
library(dplyr) # データ操作用
library(MatchIt) # マッチングを行うための主要パッケージ
library(cobalt) # バランス評価と可視化のためのパッケージ
data("birthwt")
?birthwt # 詳細確認
birthwtデータセット:
1986年にマサチューセッツ州のベイステイト医療センターで収集された、妊婦のリスク因子と新生児の体重に関するデータです(189例)。
low: 低出生体重かどうか(0=2.5kg以上, 1=2.5kg未満), age: 母親の年齢, lwt: 母親の体重(ポンド), race: 人種(1=白人, 2=黒人, 3=その他), smoke: 妊娠中の喫煙(1=あり, 0=なし)★今回の処置変数, ptl: 早産の既往回数, ht: 高血圧の既往(1=あり, 0=なし), ui: 子宮過敏症の有無, ftv: 妊娠初期の通院回数, bwt: 出生体重(グラム) ★今回の結果変数
◆データの前処理
カテゴリカル変数を因子型(Factor)に変換します。
# データの前処理 bwt_data <- birthwt %>% mutate( race = as.factor(race), smoke = as.factor(smoke), ht = as.factor(ht), ui = as.factor(ui) ) # 喫煙あり(1) vs なし(0) の人数確認 table(bwt_data$smoke)
#出力結果 0 1 115 74
4. 傾向スコアの推定とマッチング
傾向スコアを算出するためのモデル式を立てます。医学的背景知識から、喫煙習慣(smoke)は年齢、人種、体重、既往歴などに影響を受けると仮定します。matchit関数を使うことで、「傾向スコアの算出(ロジスティック回帰)」と「マッチング」を一括で行うことができます。
今回は、最も一般的な最近傍マッチング(Nearest Neighbor Matching)を行います。これは、スコアが最も近い相手を順番に1人ずつ選んでいく方法です(ペアを作れなかったデータは除外されます)。
※キャリパー(Caliper)の設定
マッチングの質を高めるため、スコアが離れすぎている相手とはペアを組まないようキャリパー(許容範囲)を設定します。 一般的には「傾向スコアの標準偏差の0.2倍」という値を設定します。この基準を用いることで、バイアスの約99%を除去できると報告されており、現在最も広く推奨されている設定値です(参考文献2)。
# 傾向スコアマッチングの実行 m.out <- matchit(smoke ~ age + lwt + race + ptl + ht + ui + ftv, data = bwt_data, method = "nearest", # 最近傍マッチング distance = "glm", # ロジスティック回帰 caliper = 0.2, # 推奨設定 ratio = 1) # 1対1マッチング
設定したモデル式を用いてロジスティック回帰を実行し、各対象者がイベント(今回は喫煙)を起こす予測確率(0~1)を算出しました。これが傾向スコアとなります。このスコアの値が近似する対象者同士でペアリングを実施しました。
| 手法名 | matchit関数での指定 (method=) | 仕組み(イメージ) | メリット | デメリット |
| 最近傍マッチング (Nearest Neighbor) |
“nearest” | スコアが最も近い相手を順番に1人ずつ選んでいく。 | 最も一般的で、直感的に理解しやすい。 |
ペアになれなかったデータは捨てられるため、サンプル数が減る。
|
| フルマッチング (Full Matching) |
“full” | 全員参加全員をいくつかの小グループに分け、重み付けをして調整する。 | データを捨てずに有効活用できるため、近年推奨されることが多い。 |
単純な1対1のペアではないため、「誰と誰がペアか」が見えにくい。
|
| 最適マッチング (Optimal Matching) |
“optimal” | 全体のスコアの差の合計が最小になるようにペアを決める。 | 最近傍法よりも、全体としてバランスの良いペアができる。 |
計算に時間がかかる。別途optmatchパッケージが必要。
|
5. バランスの評価(適合度の確認)
マッチングが上手くいったか(共変量のバランスが取れたか)を確認します。
summary(m.out)
# 出力結果(一部抜粋) Call: matchit(formula = smoke ~ age + lwt + race + ptl + ht + ui + ftv, data = bwt_data, method = "nearest", distance = "glm", caliper = 0.2, ratio = 1) Summary of Balance for All Data: #1 Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean eCDF Max distance 0.5035 0.3195 0.9223 1.3121 0.2591 0.3925 age 22.9459 23.4261 -0.0951 0.8522 0.0312 0.0952 lwt 128.1351 130.8957 -0.0817 1.4126 0.0480 0.1052 race1 0.7027 0.3826 0.7003 . 0.3201 0.3201 race2 0.1351 0.1391 -0.0117 . 0.0040 0.0040 race3 0.1622 0.4783 -0.8576 . 0.3161 0.3161 ptl 0.3108 0.1217 0.3061 2.6690 0.0473 0.1389 ht0 0.9324 0.9391 -0.0267 . 0.0067 0.0067 ht1 0.0676 0.0609 0.0267 . 0.0067 0.0067 ui0 0.8243 0.8696 -0.1189 . 0.0452 0.0452 ui1 0.1757 0.1304 0.1189 . 0.0452 0.0452 ftv 0.7568 0.8174 -0.0514 1.4537 0.0309 0.1298 Summary of Balance for Matched Data: #2 Means Treated Means Control Std. Mean Diff. Var. Ratio eCDF Mean eCDF Max Std. Pair Dist. distance 0.4294 0.4210 0.0423 1.1369 0.0171 0.1111 0.0575 age 23.2037 23.6667 -0.0917 0.7260 0.0378 0.1296 1.0897 lwt 132.1111 131.7407 0.0110 1.6596 0.0452 0.1296 0.9570 race1 0.5926 0.5741 0.0405 . 0.0185 0.0185 0.4457 race2 0.1852 0.2037 -0.0542 . 0.0185 0.0185 0.5959 race3 0.2222 0.2222 0.0000 . 0.0000 0.0000 0.1481 ptl 0.1667 0.1852 -0.0300 0.9466 0.0046 0.0185 0.4497 ht0 0.9444 0.9630 -0.0738 . 0.0185 0.0185 0.3689 ht1 0.0556 0.0370 0.0738 . 0.0185 0.0185 0.3689 ui0 0.8519 0.8519 0.0000 . 0.0000 0.0000 0.1852 ui1 0.1481 0.1481 0.0000 . 0.0000 0.0000 0.1852 ftv 0.8333 0.9444 -0.0942 1.7286 0.0525 0.2222 0.7220 Sample Sizes: #3 Control Treated All 115 74 Matched 54 54 Unmatched 61 20 Discarded 0 0
◆結果の読み方
#1 Summary of Balance for All Data:
マッチング前の全データにおけるバランスです。特に Std. Mean Diff.(標準化平均差:SMD) の列に注目します。この絶対値が 0.1 を超えていると、一般的にバランスが悪いとされます(参考文献3)。distance(傾向スコア)の差が0.9223と非常に大きく、群間に大きな偏りがあることがわかります。
# 2Summary of Balance for Matched Data:
マッチング後のデータでは、SMDは絶対値が0.1未満となり、喫煙群と非喫煙群の背景因子がほぼ均質になったことを意味します。これで、ランダムに近い比較を行うことが出来ます。
#3 Sample Sizes:
Allが元のサンプル数で、Matchedはマッチングしたサンプル数です。今回はキャリパー設定により、傾向スコアが似ている相手が見つからなかったサンプルは削除されました。これは、「比較不可能な極端なデータ」を分析から排除し、結果の妥当性を高めるための処理と言えます。
※マッチングによりサンプルサイズが減少するため、除外サンプル数や特性の明示、対象がマッチング可能な集団に限定されるなど、分析の一般性(外的妥当性)には注意が必要です。
6. 効果の推定と可視化
マッチングによって作成された「疑似的なランダム化データ」を用いて、本当に見たかった効果(妊娠中の喫煙による赤ちゃんの出生体重への影響)を推定します。また、バランスの改善度合いを可視化します。
◆効果の推定
マッチング済みのデータを抽出し、t検定(または回帰分析)を行います。
# マッチング後のデータを抽出
matched_data <- match.data(m.out)
# 2. 喫煙あり群 vs なし群 で、出生体重(bwt)を比較する
t.test(bwt ~ smoke, data = matched_data)
# 出力結果
Welch Two Sample t-test
data: bwt by smoke
t = 2.5805, df = 102.64, p-value = 0.01128
alternative hypothesis: true difference in means between group 0 and group 1 is not equal to 0
95 percent confidence interval:
84.85167 648.51870
sample estimates:
mean in group 0 mean in group 1
3145.333 2778.648
傾向スコアマッチングを行った後のデータ(各54名)を用いて、喫煙の有無による出生体重の差を検証しました。
その結果、非喫煙群の平均出生体重が 3,145g であったのに対し、喫煙群では 2,779g となり、喫煙群の方が平均で 約366g 低いことが分かりました。 t検定の結果、この差は統計的に有意でした(p = 0.011)。
年齢や人種、病歴などの背景因子を調整した上でも、妊娠中の喫煙は新生児の低出生体重の強力なリスク因子であることが示唆されました。
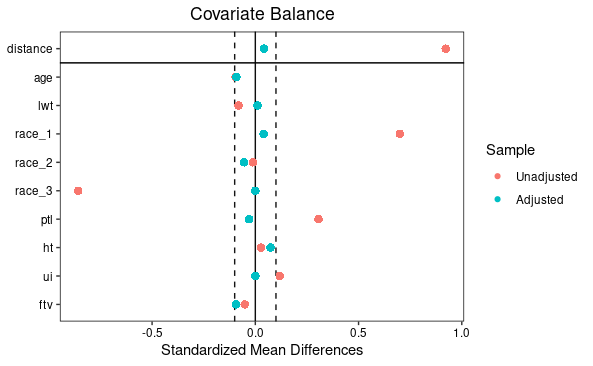
◆バランスの可視化(Love Plot)
# Love Plotで確認 love.plot(m.out, binary = "std", thresholds = c(m = .1))
◆ 図の見方
・Unadjusted(オレンジ丸):マッチング前のSMD。0.1の点線を大きく超えており、群間に大きな偏りがあったことを示します。
・Adjusted(水色丸):マッチング後のSMD。全ての変数が0.1(点線)の内側に収まっており、バイアスが取り除かれ、公平な比較が可能になったことを視覚的に示しています。
このLove Plotは傾向スコア分析の妥当性を主張するために論文等でも頻繁に用いられます。
cobaltパッケージでの図のカスタマイズは以下を参照ください。
Covariate Balance Tables and Plots: A Guide to the cobalt Package
7. まとめ
今回は、RCTの実施が難しい観察研究において、バイアスを補正して因果関係に迫る傾向スコア分析のうち、傾向スコア・マッチングについて、Rでの実装方法を解説しました。
birthwtデータセットを用いた解析では、年齢や人種、既往歴といった共変量のバランスを傾向スコア・マッチング(キャリパー付き)によって調整しました。その結果、交絡因子の影響を排除した上でも、妊娠中の喫煙は、出生体重を有意に(平均約366g)低下させるという結果が得られました。
傾向スコア分析は万能ではありませんが(未測定の交絡因子は調整できない等)、適切に使用することで、電子カルテやレセプトなどの観察データからエビデンスレベルの高い知見を導き出す強力なツールとなります。 ぜひ、MatchItやcobaltパッケージを活用して、ご自身のデータでも解析されてみてください。
参考文献
1. 星野崇宏・岡田謙介.傾向スコアを用いた共変量調整による因果効果の推定と臨床医学・疫学・薬学・公衆衛生分野での応用について.保健医療科学 2006;55:230-243.
2. Austin PC. An Introduction to Propensity Score Methods for Reducing the Effects of Confounding in Observational Studies. Multivariate Behav Res. 2011 May;46(3):399-424. doi: 10.1080/00273171.2011.568786.
3. 小川 順子, 星野 優子, 後藤 美香, 家庭部門の省エネに影響を及ぼす多様な動機に関する研究: 家庭CO2統計の個票データを用いた傾向スコアマッチングによる統計的分析, エネルギー・資源学会論文誌, 2025, 46 巻, 5 号, p. 237-248, 公開日 2025/09/10, Online ISSN 2433-0531, doi: 10.24778/jjser.46.5_237,




コメント