統計的検定は、グループ間の違いを明らかにするための重要なツールです。
二つのグループを比較する方法とそのRのコードについて、以前紹介させていただきました。
今回は、3つ以上のグループを比較する方法について紹介します。
例えば、A先生が、1組2組3組で数学の講義を行ったとします。
理解度が異なるのか？などを成績から分析してみます。
1組と2組、2組と3組、3組と1組、といったように、それぞれを2群で比較すると、検定を複数回繰り返すことによる多重検定の問題が発生してしまいます。
そこで、3つ以上のグループ間を検定回数を少なく、評価する分析法が使用されます。
この記事では、Rを使って分散分析（ANOVA）と多重比較（Tukey法）について紹介します。
1. 分散分析（ANOVA）について
2. 一元配置分散分析（one-way ANOVA）の実行と結果の解釈 ーaov関数ー
3. 多重比較（Tukey法）ーTukeyHSD関数, glht関数ー
4. 有意差表示付き箱ひげ図 ーggplot関数ー
1. 分散分析（ANOVA）
分散分析は、3つ以上のグループ間の平均値の差を評価する統計的手法です。
この手法は、正規分布に従い、等分散性を前提とするパラメトリック検定であり、以下のような場面で利用されます。
・複数の治療法や処理法の効果を比較する
・異なるグループ間の平均値の差を評価する
・複数の条件の効果を調査する
なお、正規分布に従わない場合は、ノンパラメトリック検定の手法で検定を行います。
別途記事を作成予定です。
2. 一元配置分散分析（one-way ANOVA）の実行と結果の解釈 ーaov関数ー
◆ダミーデータ作成手順
①1組2組3組のそれぞれのクラスの数学の点数データを作成（Class、Scoreの2列データ）
②①の3つのデータを行（縦）結合
※正規分布と等分散性の確認
③aov関数で分散分析
#①
n_students <- 40 #クラスの人数
set.seed(123) #乱数生成のため初期化
class_1 <- data.frame(Class = rep("1組", n_students), Score = round(rnorm(n_students, mean = 70, sd = 7), 0)) # 平均70、標準偏差7の正規分布に基づくダミーデータ
class_2 <- data.frame(Class = rep("2組", n_students), Score = round(rnorm(n_students, mean = 75, sd = 8), 0)) # 平均75、標準偏差8の正規分布に基づくダミーデータ
class_3 <- data.frame(Class = rep("3組", n_students), Score = round(rnorm(n_students, mean = 72, sd = 9), 0)) # 平均72、標準偏差9の正規分布に基づくダミーデータ
#②
library("tidyverse")
all_classes <- bind_rows(class_1, class_2, class_3) #データを縦に結合
# Class Score
#1 1組 66
#2 1組 68
#3 1組 81
#4 1組 70
#・・・
#41 2組 69
#42 2組 73
#43 2組 65
#44 2組 92
#・・・
#※正規分布と等分散性の確認
tapply(all_classes$Score, all_classes$Class, shapiro.test) # 正規分布を確認するShapiro Wilkテスト（p>0.05 正規分布）
#$`1組`
# Shapiro-Wilk normality test
#data: X[[i]]
#W = 0.98661, p-value = 0.9097
#$`2組`
# Shapiro-Wilk normality test
#data: X[[i]]
#W = 0.98752, p-value = 0.9314
#$`3組`
# Shapiro-Wilk normality test
#data: X[[i]]
#W = 0.98491, p-value = 0.8616
bartlett.test(Score ~ Class, data = all_classes) # バートレットテスト（p>0.05 等分散性）
# Bartlett test of homogeneity of variances
#data: Score by Class
#Bartlett's K-squared = 1.6317, df = 2, p-value = 0.4423
boxplot(Score ~ Class, data = all_classes, #箱ひげ図でデータを可視化※
main ="テストの点数",
xlab ="クラス", ylab ="点数",
col = "lightblue", border = "blue")
anova_result <- aov(Score ~ Class, data = all_classes) #一元配置分散分析
print(summary(anova_result))
# Df Sum Sq Mean Sq F value Pr(>F)
#Class 2 417 208.61 4 0.0209 *
#Residuals 117 6102 52.16
#Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1※箱ひげ図で可視化
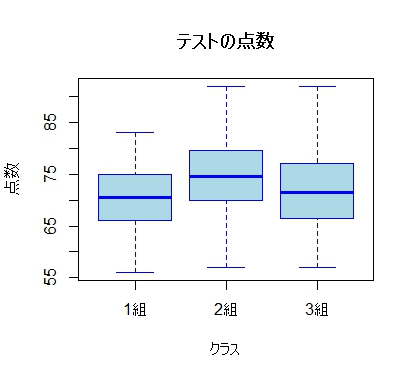
データが正規分布に従い、等分散性が確認されたため、パラメトリック検定である一元配置分散分析（ANOVA）を行いました。
Class(各クラス)の効果に関するF値は5.583であり、p値は0.0209です。
p値が有意水準（通常は0.05）よりも小さいため、少なくとも1つのクラス間には点数の平均に統計的に有意な差があることが示唆されました。どのグループ間で有意な差があったのかは、一元配置分散分析だけではわかりません。
3. 多重比較（Tukey法）ーtukeyHSD関数,glht関数ー
どのグループ間で有意な差があったのかを調べるために、多重比較を行います。
今回は、正規分布に従い、等分散性を前提とするパラメトリック検定で使用できるTukey法を紹介します。
Tukeyの多重比較では、全てのグループ間のペアごとの差を検定します。
p値が調整された形（p adj）で算出されます。
この調整されたp値は、比較を複数行う場合に生じる多重検定の問題を考慮されていて、通常はこれらの調整されたp値を基にして、各比較の有意性が評価されます。
Tukey法について2つの関数を使用したコード例（TukeyHSD関数、glht関数）を以下に示します。
tukey_result <- TukeyHSD(aov(Score ~ Class, data = all_classes)) #Tukey法 TukeyHSD関数使用
print(tukey_result)
# Tukey multiple comparisons of means
# 95% family-wise confidence level
#Fit: aov(formula = Score ~ Class, data = all_classes) #
#$Class
# diff lwr upr p adj
#2組-1組 4.525 0.6914461 8.358554 0.0162621
#3組-1組 1.725 -2.1085539 5.558554 0.5356651
#3組-2組 -2.800 -6.6335539 1.033554 0.1969696
library("multcomp")
all_classes$Class<-as.factor(all_classes$Class) #Classを因子に変更
tukey_result2<-glht(aov(Score ~ Class, data = all_classes), linfct = mcp(Class = "Tukey")) #Tukey法 glht関数使用
summary(tukey_result2)
# Simultaneous Tests for General Linear Hypotheses
#Multiple Comparisons of Means: Tukey Contrasts
#Fit: aov(formula = Score ~ Class, data = all_classes)
#Linear Hypotheses:
# Estimate Std. Error t value Pr(>|t|)
#2組 - 1組 == 0 4.525 1.615 2.802 0.0162 *
#3組 - 1組 == 0 1.725 1.615 1.068 0.5357
#3組 - 2組 == 0 -2.800 1.615 -1.734 0.1969
#---
#Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#(Adjusted p values reported -- single-step method)
2組と1組の間には平均点で統計的に有意な差があり（p<0.05）、2組の平均点が1組よりも4.525ポイント高いことが示されています。
一方、3組と1組、3組と2組の間には有意な差が見られませんでした（p > 0.05）。
これは、3組の平均点が1組および2組の平均点と統計的に有意な差がないことを示しています。
分散分析（ANOVA）と多重比較（Tukey）は、複数のグループ間の差異を評価するために広く使用される手法です。
Rを使用することで、これらの手法を簡単に実行し、結果を解釈することができます。
4. 有意差表示付き箱ひげ図 ーggplot関数ー
Tukey法で明らかとなった有意差表示を含む箱ひげ図の作成をします。
library(ggplot)
df1 <- data.frame(a = c(1, 1:3,3), b = c(109, 110, 110, 110, 109)) #有意差表示のための横棒の位置設定
df2 <- data.frame(a = c(1, 1,2, 2), b = c(99, 100, 100, 99))
df3 <- data.frame(a = c(2, 2, 3, 3), b = c(104, 105, 105, 104))
pp <- ggplot(all_classes, aes(Class, Score)) + #箱ひげ表示
geom_boxplot(aes(fill=Class))+
theme_classic()+
theme(legend.position = "none",axis.text.x=element_text(size=12), axis.text.y =element_text(size=12))
pp + geom_line(data = df1, aes(x = a, y = b)) + #有意差表示の横棒と表示情報と位置の設定
annotate("text", x = 2, y = 112, label = "n.s", size = 4) +
geom_line(data = df2, aes(x = a, y = b)) +
annotate("text", x = 1.5, y = 102, label = "*", size = 4) +
geom_line(data = df3, aes(x = a, y = b)) +
annotate("text", x = 2.5, y = 107, label = "n.s.", size = 4)
#有意差表示のための横棒の位置設定は、縦軸の数値に合わせて上記緑字部分を設定してください。
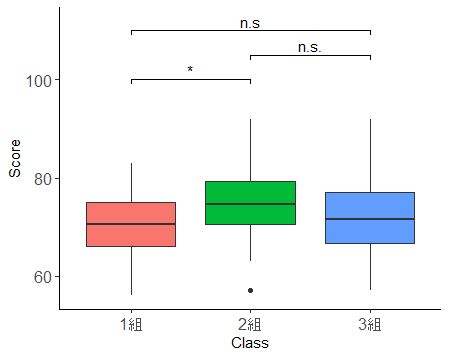
この図によって、1組と2組は平均に統計学的有意差が確認されたことが分かりやすく説明できます。
参考図書
コメント