Rで3群以上の検定（パラメトリック検定）② ー分散分析(ANOVA) + Dunnett法, Welch ANOVA + Games-Howell法ー

今回は、
・コントロールがある3群の検定（正規分布・等分散性有り）
・3群のデータが正規分布だが等分散性のない場合の検定
について紹介したいと思います。
正規分布を前提とする、パラメトリック検定になります。

先日は、正規分布・等分散性ありの3群の検定として、分散分析（ANOVA）を行い、Tukey法で多重比較（post-hoc test 事後検定）を行う方法を紹介しました。

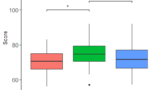
Rで3群以上の検定（パラメトリック検定）①ー分散分析(ANOVA)、多重比較(Tukey)、有意差表示付き箱ひげ図ー

統計的検定は、グループ間の違いを明らかにするための重要なツールです。今回は、3つ以上のグループを比較する方法について紹介します。例えば、A先生が、1組2組3組で数学の講義を行ったとします。理解度が異なるのか？などを成績から分...

こちらは、全条件のペア間の比較結果を算出することができました。

■目次
1.　コントロールがある3群の検定（正規分布・等分散性有り）分散分析とDunnett法
2.　3群のデータが正規分布だが等分散性のない場合の検定 Welch分散分析とGames-Howell法

1.　コントロールがある3群の検定（正規分布・等分散性有り）分散分析とDunnett法

植物の収量をあげるためにいろいろな工夫が行われます。例えば、肥料を使用したり、水の上げ方を変えたり、処理を行うことによって収量アップを検討されます。
今回は、通常の条件（コントロール）と、処理１、処理２での収量のデータをとり、そのデータ比較についてRのコード例と共に解説をしてみたいと思います。

今回使用するのは、PlantGrowthというRに含まれるデータセットです。
コントロールと2つの異なる処理条件で得られた収量（植物の乾燥重量で測定）を比較した実験の結果です。
ここでは、コントロールに対して、処理１あるいは処理２はそれぞれ平均に差があるといえるのか？を調べたいと思います。
正規分布に従うか、等分散性かの確認後、multcompパッケージのglht関数を使用し、分散分析を行い、Dunnett法で多重比較を行います。

head(PlantGrowth)
#  weight group
#1   4.17  ctrl
#2   5.58  ctrl
#3   5.18  ctrl
#4   6.11  ctrl
#5   4.50  ctrl
#6   4.61  ctrl
#※正規分布と等分散性の確認
tapply(PlantGrowth$weight, PlantGrowth$group, shapiro.test) # 正規分布を確認するShapiro Wilkテスト（p>0.05　正規分布）
#$ctrl
#	Shapiro-Wilk normality test
#data:  X[[i]]
#W = 0.95668, p-value = 0.7475
#$trt1
#	Shapiro-Wilk normality test
#data:  X[[i]]
#W = 0.93041, p-value = 0.4519
#$trt2
#	Shapiro-Wilk normality test
#data:  X[[i]]
#W = 0.94101, p-value = 0.5643
bartlett.test(Score ~ Class, data = all_classes) # バートレットテスト（p>0.05 等分散性）
#Bartlett test of homogeneity of variances
#data:  weight by group
#Bartlett's K-squared = 2.8786, df = 2, p-value = 0.2371
boxplot(weight ~ group, data =PlantGrowth)　#箱ひげ図
library(multcomp)
res<-glht(aov(weight ~ group, data = PlantGrowth), linfct = mcp(group = "Dunnett"))　#分散分析＋Dunnett多重比較
summary(res1)
#	 Simultaneous Tests for General Linear Hypotheses
#Multiple Comparisons of Means: Dunnett Contrasts
#Fit: aov(formula = weight ~ group, data = PlantGrowth)
#Linear Hypotheses:
#                　　　Estimate 　Std. Error　 t value　 Pr(>|t|)
#trt1 - ctrl == 0　  -0.3710     　0.2788  　 -1.331     0.323
#trt2 - ctrl == 0   　0.4940     　0.2788  　  1.772     0.153
#(Adjusted p values reported -- single-step method)

#箱ひげ図

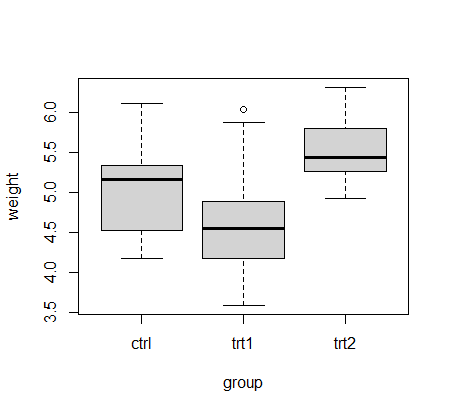
コントロール（ctrl）と処理１（trt1)、ctrlと処理２（trt2）ともに青字が示すp値は>0.05でした。
なお、こちらに示されるp値はdunnettでの多重補正による調整済みp値が表示されています。
これより、コントロールに比べると、処理１処理２ともに、収穫量に統計学的有意差があるといえない結果となりました。

2.　3群のデータが正規分布だが等分散性のない場合の検定 Welch分散分析とGames-Howell法

正規分布であり、分散が等しくないデータを作ってみます。

set.seed(123)
group1 <- rnorm(40, mean = 5, sd = 1)  # 平均値5、標準偏差1の正規分布に従うデータ
group2 <- rnorm(40, mean = 6, sd = 2)  # 平均値6、標準偏差2の正規分布に従うデータ
group3 <- rnorm(40, mean = 7, sd = 3)  # 平均値7、標準偏差3の正規分布に従うデータ

data <- data.frame(
#     weight = c(group1, group2, group3),
#     group = factor(rep(c("Group1", "Group2", "Group3"), each = 30))
tapply(data$weight, data$group, shapiro.test)  # p>0.05　正規分布
#$Group1
#	Shapiro-Wilk normality test
#data:  X[[i]]
#W = 0.98859, p-value = 0.953
#$Group2
#	Shapiro-Wilk normality test
#data:  X[[i]]
#W = 0.98791, p-value = 0.9398
#$Group3
#	Shapiro-Wilk normality test
#data:  X[[i]]
#W = 0.98674, p-value = 0.9129
bartlett.test(weight ~ group, data = data)  # p>0.05 等分散性
#	Bartlett test of homogeneity of variances
#data:  weight by group
#Bartlett's K-squared = 24.844, df = 2, p-value = 1.811e-08 #等分散性なし

上記で、正規分布だが、等分散性はない3群のデータができました。

Welchは、分散性に対して柔軟性があり、Games-Howell法も等分散性を前提としていないので、等分散性がない群の比較では、広く使用されている。
Welch分散分析＋Games-Howell法で平均値比較をしたいと思います。

library(rosetta)　#古いver.Rだと、library(userfriendlyscience)
oneway(x=data$group, y=data$weight, posthoc = 'games-howell')　#　Welch ANOVA + Games Howell
#### Oneway Anova for y=weight and x=group (groups: Group1, Group2, Group3)
#Omega squared: 95% CI = [.05; .27], point estimate = .14
#Eta Squared: 95% CI = [.06; .25], point estimate = .16
#                            　　　　　        SS　  Df 　   MS　     F 　　    p
#Between groups (error + effect)  78.34 　 2 　39.17 　10.78 　<.001
#Within groups (error only)      　425.22  117    3.63            

#### Post hoc test: games-howell
#            　　　　  diff　 ci.lo 　ci.hi  　  t  　     df         p
#Group2-Group1 0.94  0.13  　1.75 　2.81　55.29   .018
#Group3-Group1 1.98  0.95 　 3.01 　4.66　48.65  <.001
#Group3-Group2 1.04 -0.17  　2.24 　2.06　72.69   .105　#調整済みp値

この結果から、Group1と2(p=0.018, *)、Group1と３(p<0.001, ***)がp<0.05で統計学的有意差があることが分かりました。

参考サイトhttps://rpubs.com/aaronsc32/games-howell-test

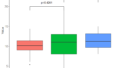
boxplot(weight ~ group, data =data)　#箱ひげ図の縦軸を確認
library(ggplot2)
df1 <- data.frame(a = c(1, 1:3,3), b = c(19, 20, 20, 20, 19))  #有意差表示のための横棒の位置設定
df2 <- data.frame(a = c(1, 1,2, 2), b = c(15, 16, 16, 15))
df3 <- data.frame(a = c(2, 2, 3, 3), b = c(17, 18, 18, 17))
pp <- ggplot(all_classes, aes(Class, Score)) + 　#箱ひげ表示
  geom_boxplot(aes(fill=Class))+
  theme_classic()+
  theme(legend.position = "none",axis.text.x=element_text(size=12), axis.text.y =element_text(size=12))
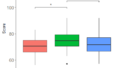
pp + geom_line(data = df1, aes(x = a, y = b)) + 　　　#有意差表示の横棒と表示情報と位置の設定
     annotate("text", x = 2, y = 20, label = "***", size = 4) +　　#p<0.05 ：*, p<0.01：**, p<0.001：***と表示
     geom_line(data = df2, aes(x = a, y = b)) + 
     annotate("text", x = 1.5, y = 16, label = "*", size = 4) +
     geom_line(data = df3, aes(x = a, y = b)) + 
     annotate("text", x = 2.5, y = 18, label = "n.s.", size = 4)

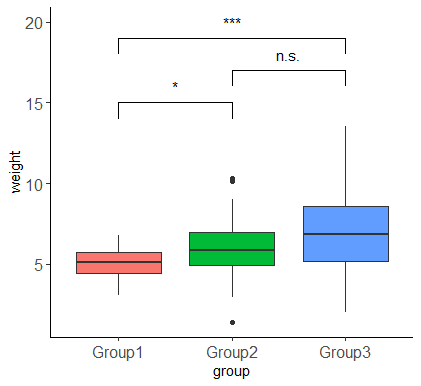
この図によって、各グループ間の平均比較において、どこのグループ間に統計学的有意差が確認されたかが分かりやすく説明できます。

Welchの分散分析とGames-Howell法を用いた事後検定の結果、Group1とGroup2、Group1とGroup3の間で統計的に有意な差が確認されました（有意水準0.05）。

データに特定の分布を前提としないノンパラメトリックの3群比較の記事も挙げていますので、参考にしていただけると幸いです。