日常のアンケートや心理テストでは、私たちはたくさんの質問に答えることがあります。
こうした多くの質問の背後には、回答の傾向に影響を与える共通の性格や思考パターンのような見えない要因が潜んでいることがあります。
このような観測できない因子をデータから統計的に推測し、構造化する方法が因子分析(Factor Analysis)です。
本記事では、心理学的な性格データを用いて、Rによる因子分析の基本的な流れと可視化の方法を、コード付きでわかりやすく紹介します。
1. 因子分析とは?
2. 使用するデータと前処理
3. 因子数の決定方法(スクリープロット)
4. 因子分析の実行(factanal関数)
5. 因子回転(Promaxなど)と結果の解釈
6. 可視化
7. まとめ
1. 因子分析とは?
因子分析は、観測された多くの変数の背後にある共通する要因(因子)を抽出する手法です。
心理テストやアンケートなど、多次元のデータの中から潜在的な構造を見つけたいときに使われます。
主成分分析との違いは、因子分析が誤差を考慮するモデルベースの手法である点です。
2. 使用するデータと前処理
psychパッケージにあるbfiデータセット(性格に関する心理尺度)を使います。
今回使うbfiデータは、性格診断テストで使われるような項目に対する回答データで、約2800人分のデータが収録されています。
質問は協調性や勤勉性など5つの性格特性に基づいて構成され、6段階の評価で答えられています。
bfiデータセット:
・25項目の性格に関する質問への回答(6段階評価:1 = 非常に当てはまらない ~ 6 = 非常に当てはまる)
5つの性格因子に基づいて分類
– 協調性(Agreeableness)
– 勤勉性(Conscientiousness)
– 外向性(Extraversion)
– 神経症傾向(Neuroticism)
– 開放性(Openness)
・性別(1 = 男性, 2 = 女性)
・最終学歴(高校卒、大学卒など)
・年齢
このデータは、因子分析や項目反応理論(IRT)の練習用デモデータとして広く使われています。
library(psych) head(bfi) # A1 A2 A3 A4 A5 C1 C2 C3 C4 C5 E1 E2 E3 E4 E5 N1 N2 N3 N4 N5 O1 O2 O3 O4 O5 gender education age #61617 2 4 3 4 4 2 3 3 4 4 3 3 3 4 4 3 4 2 2 3 3 6 3 4 3 1 NA 16 #61618 2 4 5 2 5 5 4 4 3 4 1 1 6 4 3 3 3 3 5 5 4 2 4 3 3 2 NA 18 #61620 5 4 5 4 4 4 5 4 2 5 2 4 4 4 5 4 5 4 2 3 4 2 5 5 2 2 NA 17 #61621 4 4 6 5 5 4 4 3 5 5 5 3 4 4 4 2 5 2 4 1 3 3 4 3 5 2 NA 17 #61622 2 3 3 4 5 4 4 5 3 2 2 2 5 4 5 2 3 4 4 3 3 3 4 3 3 1 NA 17 #61623 6 6 5 6 5 6 6 6 1 3 2 1 6 5 6 3 5 2 2 3 4 3 5 6 1 2 3 21 bfi_data <- na.omit(bfi[, 1:10]) # 最初の10項目のみ抽出し、欠損値を除去 summary(bfi_data) # A1 A2 A3 A4 A5 C1 C2 C3 C4 # Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.00 Min. :1.000 Min. :1.00 Min. :1.000 Min. :1.000 Min. :1.000 # 1st Qu.:1.000 1st Qu.:4.000 1st Qu.:4.000 1st Qu.:4.00 1st Qu.:4.000 1st Qu.:4.00 1st Qu.:4.000 1st Qu.:4.000 1st Qu.:1.000 # Median :2.000 Median :5.000 Median :5.000 Median :5.00 Median :5.000 Median :5.00 Median :5.000 Median :5.000 Median :2.000 # Mean :2.415 Mean :4.794 Mean :4.595 Mean :4.68 Mean :4.548 Mean :4.51 Mean :4.363 Mean :4.291 Mean :2.559 # 3rd Qu.:3.000 3rd Qu.:6.000 3rd Qu.:6.000 3rd Qu.:6.00 3rd Qu.:5.000 3rd Qu.:5.00 3rd Qu.:5.000 3rd Qu.:5.000 3rd Qu.:4.000 # Max. :6.000 Max. :6.000 Max. :6.000 Max. :6.00 Max. :6.000 Max. :6.00 Max. :6.000 Max. :6.000 Max. :6.000 # C5 # Min. :1.000 # 1st Qu.:2.000 # Median :3.000 # Mean :3.319 # 3rd Qu.:5.000 # Max. :6.000
最初の10問(A1~A5(協調性Agreeableness), C1~C5(勤勉性Conscientiousness))に絞って、因子分析を行っていきます!
A1:他人の感情に無関心である。
A2:他人の安否を気遣う。
A3:他人を慰める方法を知っている。
A4:子供を愛する。
A5:人をリラックスさせる。
C1:仕事に厳格である。
C2:完璧になるまで続ける。
C3:計画通りに物事を行う。
C4:中途半端に物事を行う。
C5:時間を無駄にする。
3. 因子数の決定方法(スクリープロット)
因子分析のための並列分析を行います。これにより、データに含まれる潜在因子の数を判断します。
fa.parallel()関数でスクリープロットを描き、因子数の目安をつけます。
fa.parallel(bfi_data, fa = "fa")
# 出力結果 # Parallel analysis suggests that the number of factors = 3 and the number of components = NA
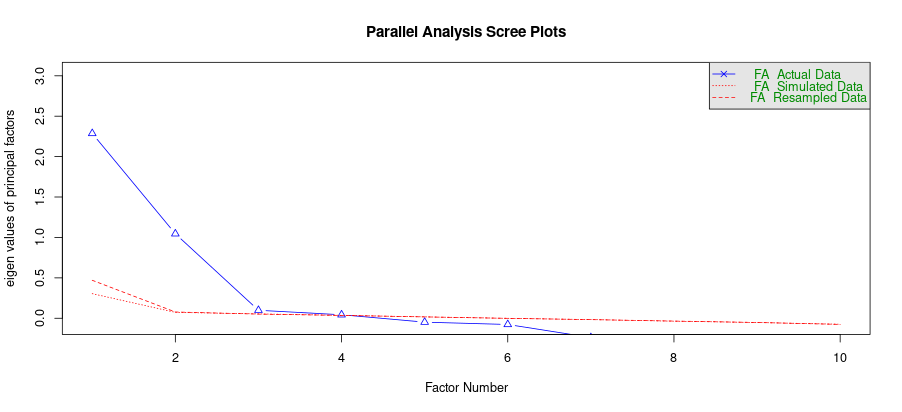
横軸:因子の番号、縦軸:主因子の固有値、青線:実データに対する固有値、赤線:ランダムに生成したデータに対する固有値
図の中で、青い線(実データの固有値)が赤い線(ランダムなデータの固有値)より上にあるところが、意味のある“因子”だと判断されます。よって、この計算より導かれる潜在因子数は3です。
※最初の10問は、協調性と勤勉性に関する質問、大きく分けると2因子とされています。しかしながら、計算では3因子と算出されました。これは、実データの分散構造に基づいた因子数の提案であり、設計とのずれは生じることはあります。
4. 因子分析の実行(factanal)
factanal()関数は、指定した因子数に基づいて因子分析を実行し、各項目がどの因子にどれだけ関係しているかを示す 因子負荷量(factor loadings) を出力します。これにより、項目の背後にある潜在的な因子構造を明らかにしていきます。
result <- factanal(bfi_data, factors = 3, rotation = "none") print(result)
# 出力結果
Call:
factanal(x = bfi_data, factors = 3, rotation = "none")
Uniquenesses:
A1 A2 A3 A4 A5 C1 C2 C3 C4 C5
0.800 0.559 0.422 0.735 0.605 0.644 0.484 0.709 0.332 0.641
Loadings:
Factor1 Factor2 Factor3
A1 -0.243 -0.296 0.232
A2 0.484 0.454
A3 0.519 0.555
A4 0.441 0.255
A5 0.457 0.430
C1 0.466 -0.274 0.254
C2 0.560 -0.290 0.343
C3 0.487 -0.203 0.114
C4 -0.660 0.391 0.283
C5 -0.543 0.226 0.115
Factor1 Factor2 Factor3
SS loadings 2.463 1.256 0.351
Proportion Var 0.246 0.126 0.035
Cumulative Var 0.246 0.372 0.407
Test of the hypothesis that 3 factors are sufficient.
The chi square statistic is 233.4 on 18 degrees of freedom.
The p-value is 1.9e-39
本結果は、rotation = “none”(回転なし)で因子分析を実施しており、出力されたFactor1〜3の因子負荷量は、そのままでは解釈が難しい構造(混合的な寄与)になっています。
例えば、A2~A5のように複数の因子にまたがって中程度の負荷を示す項目が多く、どの因子が主にその項目を代表しているのかが曖昧です。これは、スケーリング(scaling)因子、すなわち因子の座標軸の取り方が最適化されていないことを意味します。
このような状態では、因子の構造的な意味や解釈のしやすさが損なわれるため、因子軸の向きを調整する因子回転が必要です。
5. 因子回転(Promaxなど)と結果の解釈
因子回転(factor rotation)は、因子分析の結果として得られる因子負荷量の構造をより明瞭にし、解釈しやすくするための手法です。
・直交回転(例:Varimax):因子間の相関を認めず、因子を互いに独立とみなす。
・斜交回転(例:Promax):因子間の相関を認め、現実的な構造を想定する。
特に教育・心理分野では、Promax回転がよく使われます。Promax回転は因子間の相関を許容するため、より現実的な心理特性の解釈が可能になります。
result_promax <- factanal(bfi_data, factors = 3, rotation = "promax") print(result_promax)
# 出力結果 #Call: #factanal(x = bfi_data, factors = 3, rotation = "promax") #Uniquenesses: # A1 A2 A3 A4 A5 C1 C2 C3 C4 C5 #0.800 0.559 0.422 0.735 0.605 0.644 0.484 0.709 0.332 0.641 #Loadings: # Factor1 Factor2 Factor3 #A1 -0.362 0.275 0.223 #A2 0.666 #A3 0.790 #A4 0.468 0.153 #A5 0.640 #C1 0.584 #C2 0.728 #C3 0.410 -0.161 #C4 0.122 -0.123 0.781 #C5 -0.192 0.460 # Factor1 Factor2 Factor3 #SS loadings 1.847 1.193 0.913 #Proportion Var 0.185 0.119 0.091 #Cumulative Var 0.185 0.304 0.395 #Factor Correlations: # Factor1 Factor2 Factor3 #Factor1 1.000 0.254 0.593 #Factor2 0.254 1.000 0.413 #Factor3 0.593 0.413 1.000 #Test of the hypothesis that 3 factors are sufficient. #The chi square statistic is 233.4 on 18 degrees of freedom. #The p-value is 1.9e-39
Promax回転によって、
☑因子負荷量(Loadings)が明確化
回転前と比べて、各項目が1つの因子に強く寄与するように整理されました(例:A2~A5はFactor1に、C1~C3はFactor2に、C4~C5はFactor3に高い負荷)。
複数の因子にまたがる中間的な負荷が減少し、解釈しやすくなりました。
☑スケーリングの歪みが解消された
回転を行っていない場合は、質問項目が複数の因子に中途半端に関係してしまい、「どの因子が中心なのか」がわかりにくくなります。これは、因子の座標軸(スケーリング)が歪んでいる状態とも言えます。
Promax回転によってこの歪みが修正され、項目ごとの主な因子がより明確になりました。
各結果の解釈
・因子負荷量(主な特徴):
Factor1:A2〜A5 が高い正の負荷 → 協調性(Agreeableness)
Factor2:C1〜C3 が高い正の負荷 → 勤勉性(Conscientiousness)
Factor3:C4, C5 が強い負荷 → 逆方向の勤勉性(怠惰)を示す可能性
・因子の寄与率(各因子の説明する分散割合):
Factor1: 18.5%
Factor2: 11.9%
Factor3: 9.1%
累積寄与率:39.5%
・因子間の相関(斜交回転なので非ゼロ):
Factor1 と Factor3 の相関がやや高め(0.593)
・適合度検定:
カイ二乗値 = 233.4(自由度 = 18)
p値 = 1.9e-39(非常に有意)
⇒ 3因子モデルはデータに対して十分に当てはまっていると判断可能
「協調性」「勤勉性」「その逆側の傾向」といった心理的特性の構造を、10項目のデータから明確に抽出できたと考えられます。
6. 可視化
corrplotパッケージを使って因子負荷量を視覚的に表示します。
library(corrplot) library(RColorBrewer) loadings_mat <- as.matrix(result_promax$loadings) corrplot(loadings_mat, is.corr = FALSE, method = "circle", tl.col = "black", col = colorRampPalette(brewer.pal(8, "RdYlBu"))(100))
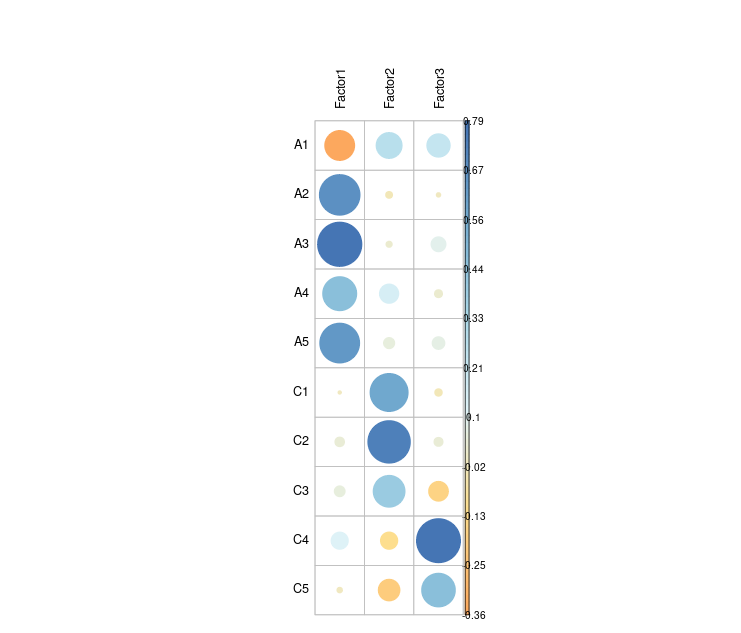
視覚的にも、各項目の因子負荷量をとらえることができました。





コメント