メタアナリシスは、複数の研究結果を統合し、より高いエビデンスレベルの結論を導き出すものです。
これまで、Rを用いて、dat.laopaiboon2015データセットに含まれる下気道感染症に対する薬剤投与に関する複数の臨床結果について、メタアナリシスに用いられる解析方法を紹介してきました。
・【Rコード付】Rでメタアナリシス①|フォレスト図と効果量:
データの統合と異質性の評価を行い、研究間の結果にばらつきがあること(高い異質性 I² ≈ 65%)を確認しました。
・【Rコード付】Rでメタアナリシス②|ファンネルプロットとEgger/Begg検定:
出版バイアスの評価を行い、ファンネルプロットではやや非対称性が見られるものの、統計テストでは明確な出版バイアスの証拠はない、という結果を得ました。
記事①で明らかになった高い異質性は、単に全体の結果を平均するだけでは不十分であることを示唆しています。
なぜ研究によって結果がこれほどばらつくのか?の原因を、深堀りすることにより、より信頼性の高い結論を導く鍵となります。
本記事では、この異質性の原因を探索するための代表的な手法であるサブグループ解析とメタ回帰について、Rでの解析方法を紹介したいと思います。
💡高い異質性が見つかったから、サブグループ解析?メタ回帰?
メタアナリシスを行う際に、サブグループ解析やメタ回帰を行うことはあらかじめ計画書に盛り込んでおく必要があります。
事前に立てた仮説を検証していく作業になりますので、結果を見ながら手法を変えたり、追加したり、、というのは、信頼性を損なうため、避ける必要があります!
今回は、あくまでも探索的な位置づけ、手法の紹介、と思っていただけますと幸いです。
1. サブグループ解析とは
サブグループ解析は、研究を特定のカテゴリカルな特性に基づいてグループ分けし、各グループ内でメタアナリシスを行う手法です。
これにより、研究間の異質性がそのグループ分けによって説明できるか、また特定のグループで効果が異なるか、などを評価できます。これは、異質性の原因を探るだけでなく、ファンネルプロットの非対称性が特定のサブグループ(例:小規模研究)に起因する「小規模研究効果」なのか、それとも出版バイアスなのかを考える上でも役立ちます。
💡どの因子をサブグループ分けに使用するか??
人口統計学的特性(年齢、性別など)、臨床的特性(疾患の重症度、病期など)、バイオマーカーなどが用いられます。
※参考文献
https://pmc.ncbi.nlm.nih.gov/articles/PMC7920926/
https://pmc.ncbi.nlm.nih.gov/articles/PMC10523858/
2. 使用パッケージとデータ
metaforパッケージのdat.laopaiboon2015(下気道感染症に対するアジスロマイシンの有効性に関する研究(15の研究結果のデータ))を使用します。
metaパッケージでサブグループ解析を、metaforパッケージでメタ回帰を、おこないます。
シンプルなコードだったので、紹介します!
## パッケージとデータ library(metafor) library(meta) head(dat.laopaiboon2015) # author year ai n1i ci n2i age diag.ab diag.cb diag.pn ctrl #1 Balmes 1991 4 48 7 56 adults 1 0 0 amoxyclav #2 Beghi 1995 22 69 2 73 adults 0 1 0 amoxyclav #3 Biebuyck 1996 53 497 53 257 adults 1 1 0 amoxyclav #4 Daniel 1991 5 121 10 120 adults 1 0 0 amoxycillin #5 Ferwerda 2001 5 55 7 53 children 0 0 1 amoxyclav #6 Gris 1996 6 34 2 33 adults 1 1 1 amoxyclav
dat.laopaiboon2015データセットには、サブグループ分けに利用できる変数として、患者が大人(adults)か子ども(children)かを示す age があります。年齢による薬の代謝の違いなどは既報もありますので、ageを用いてサブグループ解析を行います。
3. Rでサブグループ解析と可視化
#データセットの準備 dat <- dat.laopaiboon2015 #サブグループ解析の実行 m.correct.subgroup <- metabin(event.e = ai, n.e = n1i, event.c = ci, n.c = n2i, studlab = author, data = dat.laopaiboon2015, sm = "RR", random = TRUE, subgroup = age) #サブグループの変数 # 解析結果のサマリーを表示 summary(m.correct.subgroup)
#出力結果
RR 95%-CI %W(common) %W(random) age
Balmes 0.6667 [0.2077; 2.1403] 4.9 7.6 adults
Beghi 11.6377 [2.8423; 47.6496] 1.5 6.5 adults
Biebuyck 0.5171 [0.3645; 0.7336] 52.9 11.5 adults
Daniel 0.4959 [0.1747; 1.4077] 7.6 8.2 adults
Ferwerda 0.6883 [0.2328; 2.0347] 5.4 8.0 children
Gris 2.9118 [0.6324; 13.4061] 1.5 6.0 adults
Harris 1.3860 [0.4597; 4.1787] 4.0 7.9 children
Hoepelman 1.0625 [0.2814; 4.0120] 2.9 6.8 adults
Hoepelman 0.5903 [0.1475; 2.3630] 3.8 6.6 adults
Mertens 0.2000 [0.0251; 1.5917] 3.8 4.2 adults
Sevieri 2.5000 [0.5342; 11.6998] 1.5 5.9 adults
Whitlock 0.1864 [0.0094; 3.7134] 2.0 2.5 adults
Wubbel 0.6282 [0.0591; 6.6754] 1.3 3.5 children
Zachariah 1.1429 [0.4237; 3.0826] 5.3 8.5 adults
Zheng 6.6316 [1.5851; 27.7443] 1.4 6.4 adults
Number of studies: k = 15
Number of observations: o = 2496 (o.e = 1388, o.c = 1108)
Number of events: e = 254
RR 95%-CI z p-value
Common effect model 0.9208 [0.7330; 1.1566] -0.71 0.4782
Random effects model 1.0888 [0.6448; 1.8388] 0.32 0.7502
Quantifying heterogeneity (with 95%-CIs):
tau^2 = 0.5875 [0.1276; 2.5582]; tau = 0.7665 [0.3572; 1.5994]
I^2 = 63.6% [36.6%; 79.1%]; H = 1.66 [1.26; 2.19]
Test of heterogeneity:
Q d.f. p-value
38.45 14 0.0004
Results for subgroups (common effect model):
k RR 95%-CI Q I^2
age = adults 12 0.9183 [0.7222; 1.1675] 37.26 70.5%
age = children 3 0.9418 [0.4565; 1.9429] 0.90 0.0%
Test for subgroup differences (common effect model):
Q d.f. p-value
Between groups 0.00 1 0.9482
Results for subgroups (random effects model):
k RR 95%-CI tau^2 tau
age = adults 12 1.1505 [0.5966; 2.2186] 0.8484 0.9211
age = children 3 0.9306 [0.4463; 1.9406] 0 0
Test for subgroup differences (random effects model):
Q d.f. p-value
Between groups 0.18 1 0.6731
Details of meta-analysis methods:
- Mantel-Haenszel method (common effect model)
- Inverse variance method (random effects model)
- Restricted maximum-likelihood estimator for tau^2
- Q-Profile method for confidence interval of tau^2 and tau
- Calculation of I^2 based on Q
- Continuity correction of 0.5 in studies with zero cell frequencies
上記の結果には、固定効果モデル(common effect model)とランダム効果モデル(random effects model)の2種類の結果が示されています。今回は、研究間の異質性を考慮に入れたランダム効果モデルを採用し、そちらの結果について解説します。
1. 各グループ内での効果
・大人(adults)グループ (12研究): 統合したリスク比は1.15でした。しかし、95%信頼区間が [0.60; 2.22] と「1」をまたいでおり、効果において統計学的に有意であるとは言えない結果でした。
・子ども(children)グループ (3研究): 統合したリスク比は0.93でした。こちらも95%信頼区間が [0.45; 1.94] と「1」をまたいでおり、効果において統計学的に有意であるとは言えない結果でした。
2. グループ間の比較
Test for subgroup differences (random effects model) の結果が、グループ間に差があるかを直接検定したものです。p値が0.67と非常に高く、効果において統計学的に有意であるとは言えない結果でした。
3. 異質性の評価
大人のグループ内では、依然として高い異質性(I² = 70.5%)が残っています。これは、大人の中でもさらに別の要因(例:重症度や人種など)によって効果がばらついている可能性を示唆しています。
子供のグループでは、異質性が I² = 0.0% となっていますが、研究数が3つと非常に少ないため、この結果は参考程度に留めるべきです。
このメタアナリシスでは、全体として治療効果の明確な証拠はなく、患者の年齢(大人か子供か)が、その効果に影響を与えるという証拠も見つかりませんでした。
次に、この結果をフォレストプロットで可視化します。
#サブグループ解析のフォレストプロット forest(m.correct.subgroup, comb.fixed = FALSE, print.subgroup.labels = TRUE)
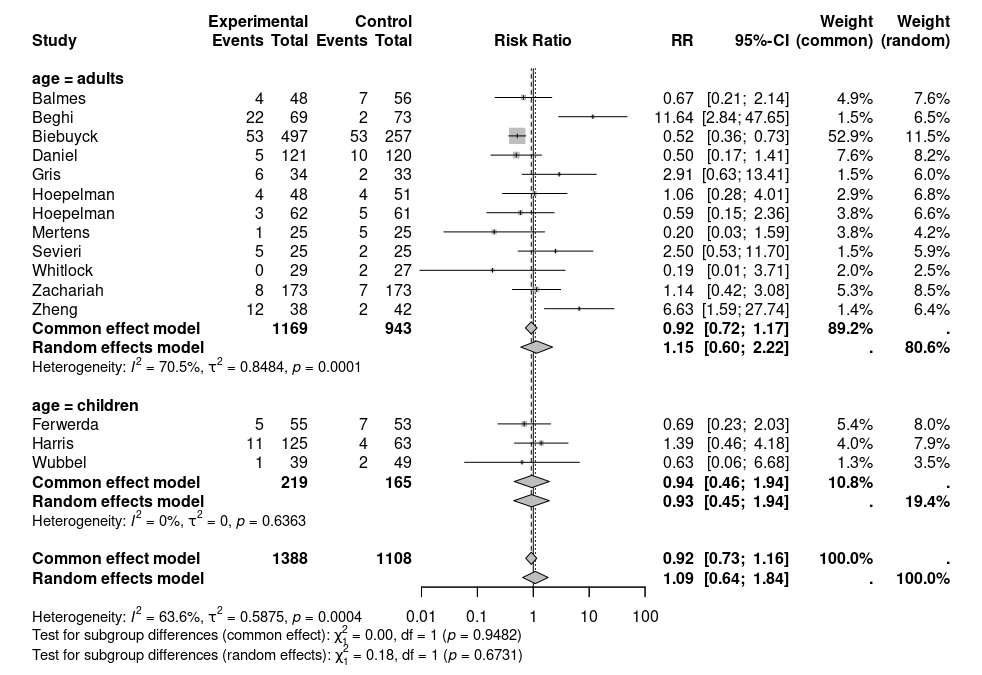
このプロットにより、大人と子どものグループごとに統合されたリスク比が計算され、視覚的に比較できます。どちらのグループの統合リスク比も、信頼区間が1をまたいでおり、有意な効果を示していないことが分かります。
4. メタ回帰とは
メタ回帰(Meta-regression)は、サブグループ解析がカテゴリカルな変数を扱うのに対し、主に連続的な変数(例:出版年、被験者の平均年齢など)と効果量との関連を調べる手法です。
「出版年が新しくなるにつれて、効果量は大きくなる(または小さくなる)傾向があるか?」といった仮説を検証できます。今回は、研究の`year`(出版年)がリスク比に影響を与えているかを調べてみましょう。
5. Rでメタ回帰と可視化
# メタ回帰の実行 library(metafor) #メタ回帰モデルを実行 res_metareg <- rma(measure="RR", ai=ai, n1i=n1i, ci=ci, n2i=n2i, data=dat.laopaiboon2015, method="REML", mods = ~ year) #出版年を引数に指定 # 解析結果のサマリーを表示 summary(res_metareg)
# 出力結果
Mixed-Effects Model (k = 15; tau^2 estimator: REML)
logLik deviance AIC BIC AICc
-19.6842 39.3685 45.3685 47.0633 48.0351
tau^2 (estimated amount of residual heterogeneity): 0.5965 (SE = 0.4099)
tau (square root of estimated tau^2 value): 0.7723
I^2 (residual heterogeneity / unaccounted variability): 65.41%
H^2 (unaccounted variability / sampling variability): 2.89
R^2 (amount of heterogeneity accounted for): 0.00%
Test for Residual Heterogeneity:
QE(df = 13) = 36.5723, p-val = 0.0005
Test of Moderators (coefficient 2):
QM(df = 1) = 1.1367, p-val = 0.2864
Model Results:
estimate se zval pval ci.lb
intrcpt -172.3299 161.7194 -1.0656 0.2866 -489.2940
year 0.0864 0.0810 1.0661 0.2864 -0.0724
ci.ub
intrcpt 144.6343
year 0.2452
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
1. モデル全体の検定
変数(今回は出版年のyear)が、全体として結果に意味のある影響を与えたかを検定する指標がTest of Moderatorsです。これは、p-val = 0.2864であり、出版年という変数は、治療効果のばらつきを説明する上で、統計学的に有意な要因ではないと判断されます。
2. 異質性
出版年のyearが、研究間のばらつき(異質性)をどれくらい説明できたかを示す指標が決定係数(R^2)です。R^2 = 0.00%であり、出版年は、研究間の異質性を全く説明できないことが示唆されます。
出版年の影響を考慮した後でも、説明できないばらつきがどれくらい残っているかを示すのがI² 統計量(I^2)です。I^2 = 65.41%であり、高い異質性が残っています。これは、出版年を考慮に入れても、ばらつきの大きさがほとんど変わらなかったことを示しています。
以前の分析で見つかった高い異質性(I² ≈ 65%)は、この出版年の影響を検証するメタ回帰によっても解決されなかった、ということになります。
# 結果をバブルプロットで可視化 regplot(res_metareg, mod="year", xlab="Publication Year (出版年)", atransf=exp, # 結果をリスク比(RR)のスケールに戻して表示 ylab="Risk Ratio", main="Meta-Regression of RR on Publication Year")
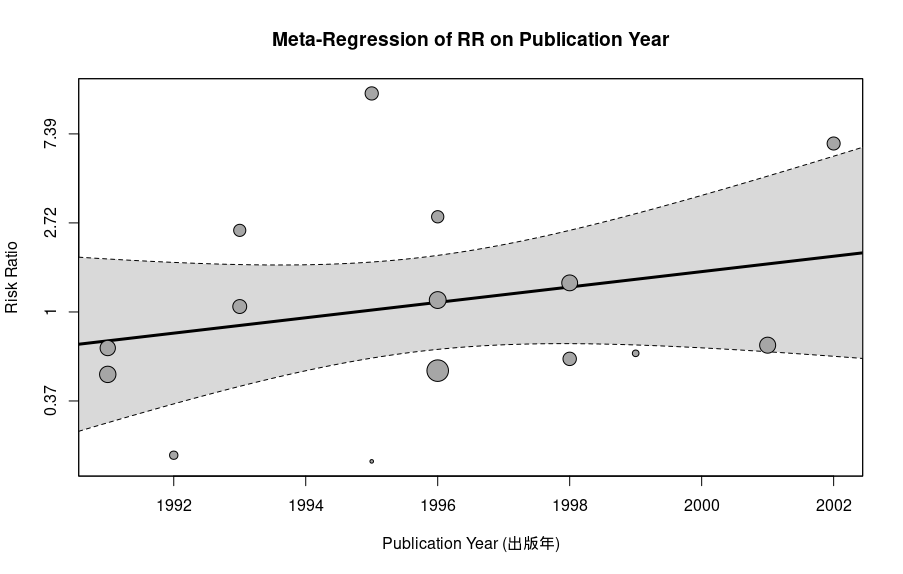
・各円(バブル): 一つ一つの研究を示します。円が大きいほど、その研究の重み(精度)が大きいことを意味します。
・横軸: 研究の出版年(1991年〜2002年)です。
・縦軸: 各研究のリスク比です。1より上なら対照薬よりリスクが高く、下ならリスクが低いことを示します。
・中央の実線: 全体の傾向を示す回帰直線です。
・グレー領域: 回帰直線の95%信頼区間です。
今回のメタ回帰分析では、「研究の出版年」が治療効果のばらつき(異質性)を説明する要因となるか検証しました。
バブルプロットの中心を貫く回帰直線は、わずかに右肩上がりの傾向を示していました。
しかしながら、直線の傾きが意味のあるものかを検定した結果(Test of Moderators)、p値は0.2864と、統計的に有意な関連性は認められませんでした。
また、グラフのグレーの領域(信頼区間)が常に「効果なし」のライン(リスク比=1)をまたいでいることからも、この傾向が非常に不確かであることが分かります。
以上より、このメタ回帰では、治療効果が研究の出版年によって変化してきたという証拠はないと結論づけられます。
6. まとめ
今回は、高い異質性の原因を探るため、サブグループ解析(年齢層別)とメタ回帰(出版年別)を行いましたが、いずれも異質性の有意な要因とはなりませんでした。
本メタアナリシスの結果、アジスロマイシンの下気道感染症に対する有効性は、対照薬と比較して統計的に有意な差があるとは言えませんでした。しかし、この結論は、原因が特定できない高い異質性を含んだものであるため、解釈には注意が必要です。異質性の原因は、今回検討した要因以外(例:対照薬の種類 ctrl、診断基準の違い など)にある可能性が考えられ、さらなる研究が望まれます。
このように、メタアナリシスは単一の統合値を出すだけでなく、異質性やバイアスを多角的に評価することで、より信頼性が高まります。ご研究に際し、メタアナリシス関連の記事を参考にしていただけますと幸いです。




コメント