「たくさんの商品について、顧客が感じているいろいろな性能の近さを可視化したい」
「日本の各都道府県の統計データ(人口密度、平均所得、日照時間など)から、『都道府県の特性の近さ』を可視化したい」
データ分析では、たくさんの変数で構成されるデータから、サンプル間の距離や類似性を理解することが重要です。しかし、数値が羅列されただけの距離一覧表から、全体の関係性を直感的に把握するのは非常に難しいです。
この記事では、そうしたサンプル間の距離情報を分かりやすく可視化する手法として、その代表例である計量MDS(Metric Multidimensional Scaling 多次元尺度構成法)について、Rのコードと共に解説していきます。
1. 計量MDS(Metric MDS)とは
2. 使用パッケージとデータ
3. Rで計量MDSを実行する
3-1. データの前処理
3-2. 計量MDSの実行と当てはまりの確認
4. 結果の可視化と解釈
5. まとめ
1. 計量MDS(Metric MDS)とは
計量MDSは、サンプル間の実際の距離(値)が、できるだけ忠実に再現されるように、サンプルを2次元や3次元のマップ上に配置する手法です。主座標分析(PCoA: Principal Coordinates Analysis)とも呼ばれ、広く使われています。
計量MDSの目的は、元のデータが持つ実際の距離の比率を維持することです。
例えば、A-B間の距離が50km、A-C間の距離が100kmなら、マップ上でもA-C間の距離がA-B間のちょうど2倍になるように表現しようと試みます。
距離の計算方法として代表的なものに、ユークリッド距離とマンハッタン距離があります。
・ユークリッド距離:2点間を直線で結んだ、最も短い距離のことです。私たちが日常的に使う「距離」の概念に最も近く、定規で測る長さに相当します。
・マンハッタン距離:碁盤の目のような経路上での距離のことです。縦と横にしか移動できない場合の最短経路を指します。
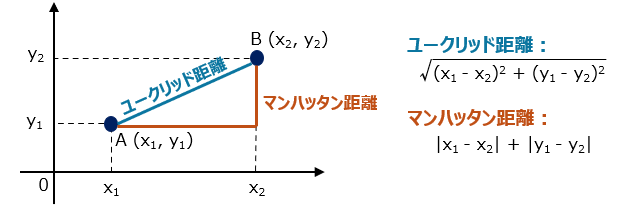
※2次元のサンプル間の距離計算式 例
※多次元だとどうなる?
n次元の点p と q の間の距離 d(p, q)は、以下の通りです。
ユークリッド距離:![]()
マンハッタン距離:![]()
次元が増える、データの変数が増えても、この式で距離を求めていくことが出来ます💡
💡主成分分析(PCA)との関係
計量MDSは、主成分分析(PCA)と深い関係があります。
PCAがデータの分散を最大化する軸を探すのに対し、計量MDSはデータ間の距離を維持する座標を探す、というアプローチの違いがあります。
異なるアプローチにもかかわらず、サンプル間の距離がユークリッド距離で計算されている場合、計量MDSの結果はPCAの結果と一致します。
2. 使用パッケージとデータ
計量MDSは、Rに標準で備わっているstatsパッケージのcmdscale()関数で実行できます。
palmerpenguinsパッケージに含まれるpenguinsデータセットを使用します。
💡penguinsデータセット
南極のパーマー諸島に生息する3種類のペンギン、合計344羽の観察データです。各変数は以下の通り。
species:ペンギンの種類、island:ペンギンが観測された島、bill_length_mm:くちばしの長さ(mm)、bill_depth_mm:くちばしの高さ(mm)、flipper_length_mm:翼の長さ(mm)、body_mass_g:体重(g)、sex:性別、year:観測年
# 1. パッケージをインストール(初回のみ)
# install.packages("palmerpenguins")
# install.packages("ggplot2")
# ライブラリを読み込む
library(palmerpenguins) #データセットpenguins用
library(ggplot2) #可視化用
head(penguins)
# 出力結果 species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g sex year 1 Adelie Torgersen 39.1 18.7 181 3750 male 2007 2 Adelie Torgersen 39.5 17.4 186 3800 female 2007 3 Adelie Torgersen 40.3 18.0 195 3250 female 2007 4 Adelie Torgersen NA NA NA NA < NA> 2007 5 Adelie Torgersen 36.7 19.3 193 3450 female 2007 6 Adelie Torgersen 39.3 20.6 190 3650 male 2007
3. Rで計量MDSを実行する
各ペンギンのくちばしの長さ・高さ、翼の長さ、体重といった複数の数値情報を用いて、ペンギン同士がどれだけ似ているかを分析します。
計量MDSは、この個体間の類似度を、2次元マップ上の点と点の間の距離として視覚的に表現する手法であり、マップ上で近くにプロットされたペンギンほど、身体的な特徴が似ていると解釈できます。
3-1. データの前処理
# 欠損値(NA)が含まれる行は分析の妨げになるため、na.omit()で削除
penguins_clean <- na.omit(penguins)
# 距離計算に使う、数値の測定データのみを抽出
penguins_numeric <- penguins_clean[, c("bill_length_mm", "bill_depth_mm", "flipper_length_mm", "body_mass_g")]
# scale()関数でデータを標準化
#'body_mass_g'(体重)のように数値のスケールが極端に大きい変数が、分析結果を支配するのを防ぐため
penguins_scaled <- scale(penguins_numeric)
head(penguins_scaled)
# 出力結果 # bill_length_mm bill_depth_mm flipper_length_mm body_mass_g #1 -0.8946955 0.7795590 -1.4246077 -0.5676206 #2 -0.8215515 0.1194043 -1.0678666 -0.5055254 #3 -0.6752636 0.4240910 -0.4257325 -1.1885721 #5 -1.3335592 1.0842457 -0.5684290 -0.9401915 #6 -0.8581235 1.7444004 -0.7824736 -0.6918109 #7 -0.9312674 0.3225288 -1.4246077 -0.7228585
3-2. 計量MDSの実行と当てはまりの確認
cmdscale()関数を使って計量MDSを実行します。k = 2で「2次元のマップの作成」を指定し、eig = TRUEでモデルの当てはまり具合を評価するための情報(固有値)も計算させます。
# ステップ1: 標準化したデータから、サンプル間のユークリッド距離行列を計算
penguins_dist <- dist(penguins_scaled)
# penguins_dist_manhattan <- dist(penguins_scaled, method = "manhattan") #マンハッタン距離の場合は、このコード
# ステップ2: 計量MDSを実行 ## eig=TRUEを指定し、座標($points)と固有値($eig)の両方算出 mds_result <- cmdscale(penguins_dist, k = 2, eig = TRUE)
# 計量MDSの座標情報のみを抽出し、ペンギンの種類の列を追加 mds_points <- as.data.frame(mds_result$points) colnames(mds_points) <- c("Dim1", "Dim2") mds_points$species <- penguins_clean$species head(mds_points)
# 出力結果
# Dim1 Dim2 species
#1 -1.850808 -0.03202119 Adelie
#2 -1.314276 0.44286031 Adelie
#3 -1.374537 0.16098821 Adelie
#4 -1.882455 0.01233268 Adelie
#5 -1.917096 -0.81636958 Adelie
#6 -1.770356 0.36567266 Adelie
計量MDSで計算された、各ペンギンが2次元マップ上で配置されるべきX座標(1列目)とY座標(2列目)が追加されました。あとで、ペンギンの種類ごとでの配置状況を確認するために、各サンプルに対応したペンギンの種類(species)情報も追加しています。
2次元マップによる、距離情報の当てはまりについても確認します。
## 固有値を取得
eigenvalues <- mds_result$eig
## 最初の2次元までの寄与率を計算
explained_variance <- sum(eigenvalues[1:2]) / sum(eigenvalues[eigenvalues > 0])
explained_variance
# 出力結果
#[1] 0.8808682
寄与率は約88.1%となりました。これは、ペンギン個体間の距離情報のうち、約88%をこの2次元マップで説明できていることを意味し、かなり良い当てはまりだと判断できます。
4. 結果の可視化と解釈
それでは、実際に座標をプロットしてみましょう。
# ggplot2でプロット
ggplot(mds_points, aes(x = Dim1, y = Dim2, color = species)) +
geom_point(size = 3, alpha = 0.8) +
labs(title = "MDS Plot",
color = "Species"
) +
theme_test() + # 図の表示の仕方指定
stat_ellipse(level = 0.95) + # 95%信頼区間の楕円を追加
coord_fixed() # 縦横比を1:1に固定し、距離の歪みをなくす
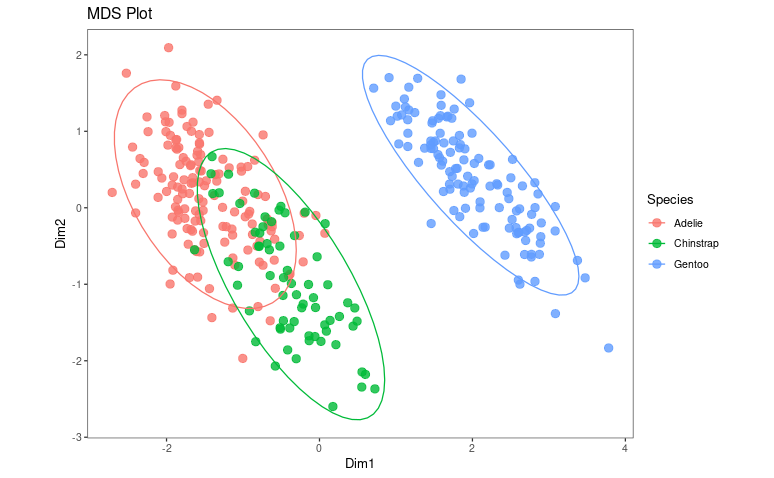
このグラフは、各ペンギンの身体測定値から計量MDSで計算された個体間の近さを、2次元空間上の点として表現しています。同じ種類(同じ色)のペンギンが近くに集まっており、種類ごとに明確なグループが形成されていることが分かります。特に、Gentoo(青)は他の2種から大きく離れた位置に集まっており、身体的な特徴が最も異なっていることが示唆されました。一方で、Adelie(赤)とChinstrap(緑)のグループは互いに近く、わずかに重なり合っていることから、この2種はGentooよりも身体的特徴が似ていることが分かりました。
5. まとめ
今回は、サンプル間の実際の距離に基づいて、その関係性を地図のように可視化する計量MDS(PCoA)について、Rでの実装方法を解説しました。
・計量MDSで、「サンプル × 変数」のデータから「距離行列」を作成し、その距離の比率をできるだけ忠実に2次元マップ上に再現しました。
・Rでは、データの標準化 scale()、距離行列の計算dist()、MDSの実行cmdscale() というステップで分析を進めました。
・penguinsデータセットで、計量MDSのプロットにより身体的特徴が似ているペンギンが近くに集まる様子が明確に可視化され、種類ごとの違いを確認でできました。
このように、計量MDSは多次元データの中に隠れた構造を視覚的にわかりやすい”距離”で捉えるための強力なツールです。
次回は、もう一つのMDSである非計量MDS(NMDS)について解説します。



コメント