3群以上の平均比較で、ノンパラメトリック検定を行います。
ノンパラメトリック検定とは、データが特定の分布（例えば正規分布）に従うという仮定を必要としない統計的手法をいいます。
データの順位や順序などに基づいて計算され、中央値の比較を行っています。
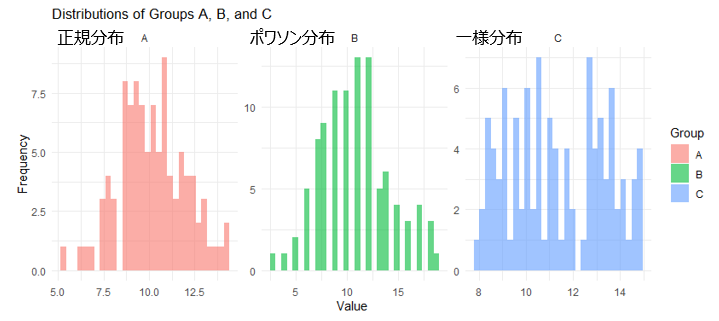
1. データの分布例の紹介(正規分布、ポアソン分布、一様分布)
2. Kruskal-Wallis検定
3. Dunn検定＋多重比較補正（Bonfferoni）
4. Dunn検定＋多重比較補正（Holm）
1. データの分布例の紹介(正規分布、ポアソン分布、一様分布)
取り扱うデータが従う分布を理解することで、それぞれに適した解析方法などを選択し、より正確な判断をすることができます。
代表的な3つの分布である正規分布、ポアソン分布、一様分布のそれぞれの特徴を説明します。
・正規分布 (Normal Distribution)
平均値を中心とした対称的なベル型の分布です。多くの自然現象や測定データは、この分布に従うことが多いです。正規分布は平均（μ）と標準偏差（σ）によって定義されます。
☆特徴
平均値を中心に左右対称
データの約68%が平均値±1標準偏差の範囲内に存在
データの約95%が平均値±2標準偏差の範囲内に存在
・ポアソン分布 (Poisson Distribution)
一定の時間や空間において一定の平均発生率でランダムに発生する事象の分布です。例えば、電話の着信回数や交通事故の発生回数などがこれに当たります。
ポアソン分布は平均発生率（λ）によって定義されます。
☆特徴
事象が稀であるほどポアソン分布に近くなる
ポアソン分布は整数値（例えば、0回、1回、2回など）のデータ（離散データ）を扱う
λが大きくなると正規分布に近くなる
・一様分布 (Uniform Distribution)
指定された範囲内のすべての値が等しい確率で発生する分布です。均等にランダムなデータを生成する際に使用されます。
☆特徴
最小値と最大値の範囲内で一様に分布
すべての値が等しい確率で現れる
set.seed(123)
group_A <- rnorm(100, mean = 10, sd = 2) # 正規分布 (mean = 10, sd = 2) sd標準偏差
group_B <- rpois(100, lambda = 11) # ポアソン分布 (lambda = 10)
group_C <- runif(100, min = 8, max = 15) # 一様分布 (min = 5, max = 15)
#groupA～Cを合わせて、3群の分布が異なるダミーデータ作成
data <- data.frame(
Value = c(group_A, group_B, group_C),
Group = rep(c("A", "B", "C"), each = 100)
)
library(ggplot2) #作図
ggplot(data, aes(x = Value, fill = Group)) +
geom_histogram(alpha = 0.6, position = "identity", bins = 30) +
facet_wrap(~ Group, scales = "free") +
theme_minimal() +
labs(title = "Distributions of Groups A, B, and C",
x = "Value",
y = "Frequency")
3群以上のパラメトリック検定については以下の記事を参照ください。
2. Kruskal-Wallis検定
Kruskal-Wallis検定は、3群以上のグループ間で中央値が等しいかどうかを比較するためのノンパラメトリック検定です。
この検定は、データが正規分布に従わない場合や、等分散性が満たされない場合に使用されます。
各群のデータを順位に変換し、その順位の合計を計算します。対象の群でこの順位の合計に差があるかどうかを検定します。
kruskal.test(Value ~ Group, data = data)
# Kruskal-Wallis rank sum test
#data: Value by Group
#Kruskal-Wallis chi-squared = 12.404, df = 2, p-value = 0.002026p値は0.002026で、有意水準0.05以下であったため、3群の中央値が全て等しいとは言えない結果であることが分かりました。
※どの群間に統計学的有意差があるかはわからない
分布が不明な場合は、Shapiro testなどで確認してください。
tapply(data$Value, data$Group, shapiro.test)
3. Dunn検定＋多重比較補正（Bonfferoni）
この検定では、まずデータを順位に変換し、それぞれの群の組み合わせについて順位和を計算します。
そして、順位和の差異に基づいて統計的な有意差を評価します。
Dunn検定は、多重比較の際にボンフェローニ（Bonferroni）補正や他の補正法を適用し、結果を解釈されることが一般的です。
library(dunn.test)
dunn.test(data$Value, data$Group, method = "bonferroni", altp=T) #Dunn検定、Bonferroni補正 altp=Tで両側検定
# Kruskal-Wallis rank sum test
#data: x and group
#Kruskal-Wallis chi-squared = 12.4037, df = 2, p-value = 0
# Comparison of x by group
# (Bonferroni)
#Col Mean-|
#Row Mean | A B
#---------+----------------------
# B | -1.468306
# | 0.4261
# |
# C | -3.506488 -2.038182
# | 0.0014* 0.1246
#alpha = 0.05
#Reject Ho if p <= alpha
#作図
boxplot(Value ~ Group, data =data) #箱ひげ図の縦軸を確認
df1 <- data.frame(a = c(1, 1:3,3), b = c(23, 24, 24, 24, 23)) #有意差表示のための横棒の位置設定
df2 <- data.frame(a = c(1, 1,2, 2), b = c(19, 20, 20, 19))
df3 <- data.frame(a = c(2, 2, 3, 3), b = c(21, 22, 22, 21))
library(ggplot2)
pp <- ggplot(data, aes(Group, Value)) + #箱ひげ表示
geom_boxplot(aes(fill=Group))+
theme_classic()+
theme(legend.position = "none",axis.text.x=element_text(size=12), axis.text.y =element_text(size=12))
pp + geom_line(data = df1, aes(x = a, y = b)) + #有意差表示の横棒と表示情報と位置の設定
annotate("text", x = 2, y = 25, label = "p=0.0014*", size = 4) +
geom_line(data = df2, aes(x = a, y = b)) +
annotate("text", x = 1.5, y = 21, label = "p=0.4261", size = 4) +
geom_line(data = df3, aes(x = a, y = b)) +
annotate("text", x = 2.5, y = 23, label = "p=0.1246", size = 4)
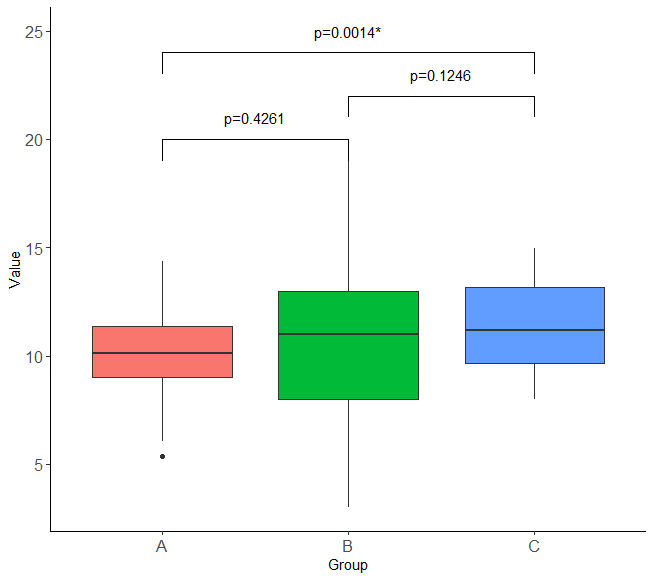
Dunn検定を行い、Bonferroniで多重比較の補正を行いました。
Kruskal-Wallis rank sum testで、p値＝０の表示であり、少なくとも1つのグループ間に有意な差があり、3群の中央値は等しいとは言えないことが分かります。
緑字の箇所は、各対比較のz検定統計量（比較値 (Col Mean-Row Mean) 上）とそれぞれのp値（下）を表示しています。
- Comparison A-B: p値 = 0.4261（p>0.05、帰無仮説を棄却せず）
- Comparison A-C: p値 = 0.0014（p<0.05、帰無仮説を棄却、統計学的有意差ないとは言えない）
- Comparison B-C: p値 = 0.1246（p>0.05、帰無仮説を棄却せず)
AとC間の中央値に統計学的有意差がないとは言えない結果でした。
※アスタリスク*は帰無仮説棄却の有意水準以下であった場合つきます。
#作図
4. Dunn検定＋多重比較補正（Holm)
> dunn.test(data$Value, data$Group, method = "Holm", altp=T)
# Kruskal-Wallis rank sum test
#data: x and group
#Kruskal-Wallis chi-squared = 12.4037, df = 2, p-value = 0
# Comparison of x by group
# (Holm)
#Col Mean-|
#Row Mean | A B
#---------+----------------------
# B | -1.468306
# | 0.1420
# |
# C | -3.506488 -2.038182
# | 0.0014* 0.0831
#alpha = 0.05
#Reject Ho if p <= alphaDunn検定を行い、Holmで多重比較の補正を行いました。
- Comparison A-B: p値 = 0.1420（p>0.05、帰無仮説を棄却せず）0.
- Comparison A-C: p値 = 0.0014（p<0.05、帰無仮説を棄却、統計学的有意差あり）
- Comparison B-C: p値 = 0.0831（p>0.05、帰無仮説を棄却せず)
こちらの手法でも、AとC間の中央値に統計学的有意差がないとは言えない結果となりました。
ノンパラメトリック検定では、データを順位に変換することで、分布の影響を受けず、検定を行うことができます。
参考資料：
dunn.test CRAN, https://cran.r-project.org/web/packages/dunn.test/dunn.test.pdf
コメント