例えば、数学のテストでXクラスとYクラスで平均点に差があるのか？ないのか？を調べたいとします。
このクラスの点数は、他のクラスと比べて差があるのか？？？
これは、XクラスとYクラスが異なる学生からなり、それぞれが受けた数学のテストの点数を比較しますので、”対応のない”2群の検定を行います。
”対応のない”2群の検定を行う場合は、2群のデータは正規性があるのか？2群のデータは等分散性があるのか？を確認してから、検定方法を決める必要があります。
| 正規性 | 等分散性 | 選択手法 |
| ◯ | ◯ | Student t 検定 |
| ◯ | × | Welch’s t 検定 |
| × | × | Man Whitney U 検定 （= Wilcoxon signed-rank 検定） |
データに正規性がある場合は、Student t検定、あるいはWelch’ｓt検定です。
以下をご参照ください。
正規性がない場合は、Man Whitney U検定（マンホイットニーU検定）（=Wilcoxon Rank-Sum 検定（ウィルコクソンの順位和検定））を用います。
同一人物が受けた異なるテストの比較などは、”対応のある”2群のt検定を行います。下記をご参照ください。
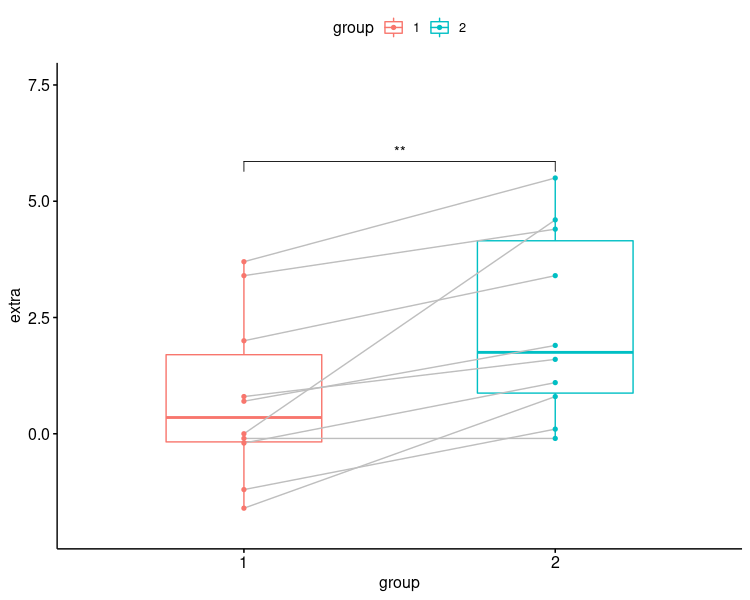
1. 2群の正規性（シャピロ・ウィルク検定）と2群間の等分散性（F検定）を確認
2. 2群が正規分布でなく、等分散でない。Mann-Whitney U検定
3. Rでプレゼンテーション ーMann-Whitney U検定, 箱ひげ図とバイオリンプロットー
1. 2群の正規性（シャピロ・ウィルク検定）と2群間の等分散性（F検定）を確認
| 正規性 | 等分散性 | 選択手法 |
| ◯ | ◯ | Student t 検定 |
| ◯ | × | Welch’s t 検定 |
| × | × | Man Whitney U 検定 （= Wilcoxon signed-rank 検定） |
正規性はシャピロ・ウィルク検定で、分散性の差はF検定で確認できます。以下に方法を記載していきます。
X<-c(50,90,86,76,84,96,84,95,96) Y<-c(5,10,50,73,80,80,80) #1 shapiro.test(X) #2 Shapiro-Wilk normality test data: X W = 0.7902, p-value = 0.01577 shapiro.test(Y) #2 Shapiro-Wilk normality test data: Y W = 0.77272, p-value = 0.02178 var.test(x=X,y=Y) #3 F test to compare two variances data: X and Y F = 0.18565, num df = 8, denom df = 6, p-value = 0.03296 alternative hypothesis: true ratio of variances is not equal to 1 95 percent confidence interval: 0.0331544 0.8635972 sample estimates: ratio of variances 0.1856521
#1 Xクラスは9名、Yクラスは7名がテストを受け、それぞれの点数をデータをいれました。ダミーデータです。
#2 シャピロ・ウィルク検定。p-value<0.05で、正規性に従うといえない。p-value≧0.05で正規性に従う。 ⇒ X,Yともに正規性に従わない。
※正規性が確認できた場合は、分散性を確認してStudent t検定あるいはWelch’s t 検定を実施します。下記をご参照ください。
#3 分散性を確認するF検定。p-value<0.05であれば、分散性に差がないといえない。p-value≧0.05であれば、分散性が差がない。 ⇒2群間は等分散ではない。
2. 2群が正規分布でなく、等分散でない。Mann-Whitney U検定
wilcox.test(X, Y) #4 Wilcoxon rank sum test with continuity correction data: X and Y W = 55.5, p-value = 0.01241 alternative hypothesis: true location shift is not equal to 0
#4 Mann-Whitney U検定を行いました。p-value<0.05 なので帰無仮説「2群の平均に差がない」が棄却され、XとYは差があると結論づけます。
データの可視化を行います。
name1<-c("X","X","X","X","X","X","X","X","X") #5
D1 <- data.frame(Class=name1, Score=X)
name2 <-c("Y","Y","Y","Y","Y","Y","Y")
D2 <- data.frame(Class=name2, Score=Y)
D3<-rbind(D1, D2)
library(ggplot2)
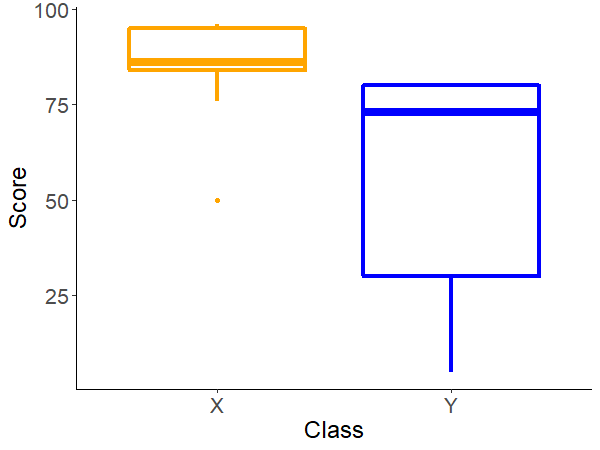
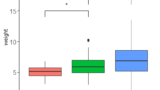
ggplot(D3, aes(x=Class, y=Score,color=Class)) + geom_boxplot(lwd=1.5)+theme_classic()+ theme(axis.text=element_text(size=16),axis.title=element_text(size=18),legend.position = "none")+scale_color_manual(values = c("orange", "blue")) #6 箱ひげ図
library(ggpubr)
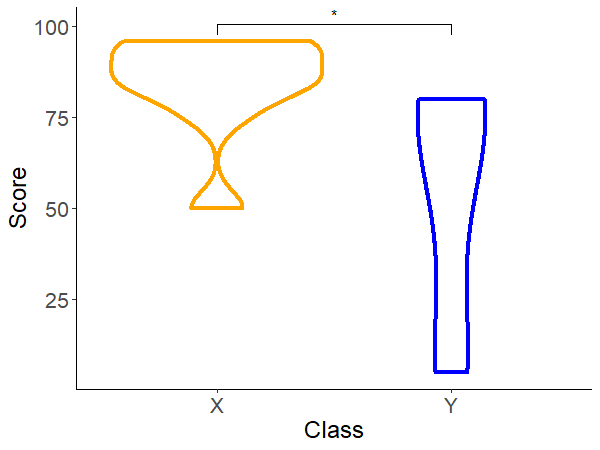
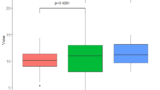
ggplot(D3, aes(x=Class, y=Score,color=Class)) + geom_violin(lwd=1.5)+theme_classic()+stat_compare_means(comparisons = list(c("X", "Y")),label = "p.signif",method = "wilcox.test")+theme(axis.text=element_text(size=16),axis.title=element_text(size=18),legend.position = "none")+scale_color_manual(values = c("orange", "blue")) #9 バイオリンプロット
#5 ggplotでの作業を行いやすいよう、XとYのデータを結合しました。Classという名の列に、Xの名前を入れ、Scoreという名の列にX組の生徒の点数を入れたdata.frameを作成しました。
#6 箱ひげ図の作成
#7 バイオリンプロットの作成
library(ggpubr)は、インストールされていなければ、install.package(ggpubr)をお願いします。
stat_compare_means()で、下記のように有意差表示を行うことができます。
4. Rでプレゼンテーション ーMann-Whitney U検定, バイオリンプロットー
コメント