AをB、C、Dなどの複数の要因で予測したいという場合に、重回帰分析が用いられます。
例えば、住宅の価格(目的変数)を、町ごとの一人当たり犯罪率、1940年以前に建てられた持ち家の割合、ボストンの5つの雇用中心地までの距離の加重平均のデータ(説明変数)から予測してみます。


1. 重回帰分析
重回帰とは、1つの目的変数を複数の説明変数で予測するものです。
1つの目的変数を1つの説明変数で予測するものは、単回帰と呼び、以下のサイトで説明していますので、こちらも御覧頂けたらと思います。
被説明変数 (応答変数, 従属変数, 目的変数) y: 説明される変数
説明変数 (独立変数, 予測変数) x: 説明する変数
説明変数がp個ある場合は、以下のモデル(線形重回帰モデル)になります。
yi=β0+β1xi1+β2Xi2+・・・+βpxip+εi
β1, β2,…βpを偏回帰係数、εi 誤差項といいます。
2. 重回帰分析をやってみよう(Bostonのデータセット使用)
今回使用するデータセットのBostonは、Housing Values in Suburbs of Boston(ボストン近郊の住宅価格)と、町ごとの一人当たり犯罪率、25,000平方フィート以上の区画に分類される住宅地の割合などの情報が含まれます。
library(MASS)
head(Boston) #1 Bostonデータセット
crim zn indus chas nox rm age dis rad tax ptratio black lstat medv
1 0.00632 18 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 396.90 4.98 24.0
2 0.02731 0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 396.90 9.14 21.6
3 0.02729 0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 392.83 4.03 34.7
4 0.03237 0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 394.63 2.94 33.4
5 0.06905 0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 396.90 5.33 36.2
6 0.02985 0 2.18 0 0.458 6.430 58.7 6.0622 3 222 18.7 394.12 5.21 28.7
Boston_lm<-lm(medv~crim+zn+indus+chas+nox+rm+age+dis+rad+tax+ptratio+black+lstat, data=Boston) #2重回帰
summary(Boston_lm) #3
Call:
lm(formula = medv ~ crim + zn + indus + chas + nox + rm + age +
dis + rad + tax + ptratio + black + lstat, data = Boston)
Residuals:
Min 1Q Median 3Q Max
-15.595 -2.730 -0.518 1.777 26.199
Coefficients:
Estimate Std.Error t value Pr(>|t|)
(Intercept) 3.646e+01 5.103e+00 7.144 3.28e-12 ***
crim -1.080e-01 3.286e-02 -3.287 0.001087 **
zn 4.642e-02 1.373e-02 3.382 0.000778 ***
indus 2.056e-02 6.150e-02 0.334 0.738288
chas 2.687e+00 8.616e-01 3.118 0.001925 **
nox -1.777e+01 3.820e+00 -4.651 4.25e-06 ***
rm 3.810e+00 4.179e-01 9.116 < 2e-16 ***
age 6.922e-04 1.321e-02 0.052 0.958229
dis -1.476e+00 1.995e-01 -7.398 6.01e-13 ***
rad 3.060e-01 6.635e-02 4.613 5.07e-06 ***
tax -1.233e-02 3.760e-03 -3.280 0.001112 **
ptratio -9.527e-01 1.308e-01 -7.283 1.31e-12 ***
black 9.312e-03 2.686e-03 3.467 0.000573 ***
lstat -5.248e-01 5.072e-02 -10.347 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 4.745 on 492 degrees of freedom
Multiple R-squared: 0.7406, Adjusted R-squared: 0.7338
F-statistic: 108.1 on 13 and 492 DF, p-value: < 2.2e-16
#1 Bostonデータセット
crim:町ごとの一人当たり犯罪率
zn:25,000平方フィート以上の区画に分類される住宅地の割合
indus:町ごとの非小売業用地面積の割合
chas:チャールズリバーのダミー変数(川に面している場合は1、そうでない場合は0)
nox:窒素酸化物濃度(1千万分の1)。
rm:1住戸当たりの平均部屋数。
age:1940年以前に建てられた持ち家の割合。
dis:ボストンの5つの雇用中心地までの距離の加重平均
rad:放射状高速道路へのアクセスの指数
tax:1万ドルあたりの固定資産税の割合。
ptratio:町ごとの生徒と教師の比率
black:1000(Bk – 0.63)^2 ただし、Bkは町ごとの黒人の割合。
lstat:人口の下位ステータス(%)。
medv:持ち家の中央値(単位:千円)。
#2 重回帰
#3 重回帰の結果表示
lm(目的変数~説明変数1+説明変数2+説明変数3・・・, data= )
β0は3.646e+01 、crimの偏回帰係数は-1.080e-01 、znは4.642e-02、indusは2.056e-02、chasは2.687、noxは-1.777e+01 、rmは 3.810、ageは 6.922e-04、disは-1.476、radは3.060e-01 、taxは-1.233e-02 、ptratioは-9.527e-01、blackは9.312e-03、lstatは-5.248e-01で、medv(yi)は、以下のようなモデル式ができます。
yi=3.646e+01-1.080e-01xi1+4.642e-02xi2+2.056e-02xi3+ 2.687xi4-1.777e+01xi5+3.810xi6+6.922e-04xi7-1.476exi8+3.060e-01xi9-1.233e-02xi10-9.527e-01xi11+9.312e-03xi12-5.248e-01xi13
Multiple R-squared(決定係数): 0.7406
Adjusted R-squared(自由度調整済み決定係数 変数の数で補正): 0.7338
これらの決定係数は、0~1の間の値をとり、モデルがどの程度yを説明できているかを示す指標になります。
p-value(p値): < 2.2e-16 で、0.05以下であるため、xがyを説明する力が十分であると結論できました。
CoefficientsにおけるPr(>|t|)は、モデル式における各因子の係数のp値を示します。
例えば、indusは0.738288、ageは0.958229であり、p>0.05で信頼できる係数では無いことがわかりました。
このように複数の因子から予測する際に、全ての因子を用いずとも、当てはまりの良い因子選択を行い、モデル式を作成する方法もあります。
これを変数選択と呼び、また別の機会に解説記事を書く予定です。
3.重回帰の当てはまり具合を、残差分析で確認(残差プロット, Q-Qプロット)
plot(Boston_lm, which=1:2) #4 残差分析
#9 残差分析の1:残差プロットと2:Q-Qプロットを指定しています。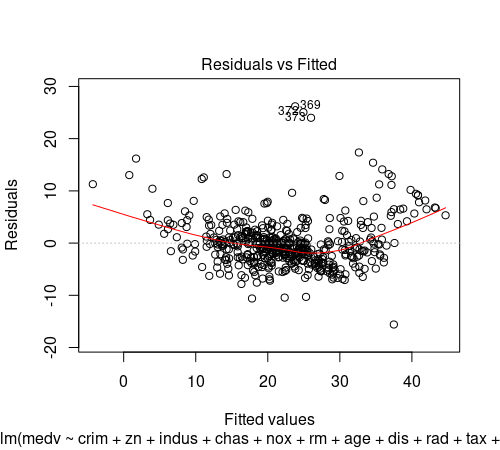
★残差プロット(上記左図)
横軸に予測値、縦軸に残差をプロットしています。
赤線は残差を説明する回帰曲線で、残差=0と重なっているほど、あてはまりがよい回帰モデルであるといえます。
図中の369、372、373 は、データフレームの行番号であり、このデータが、残差の絶対値が大きいもの※になります。
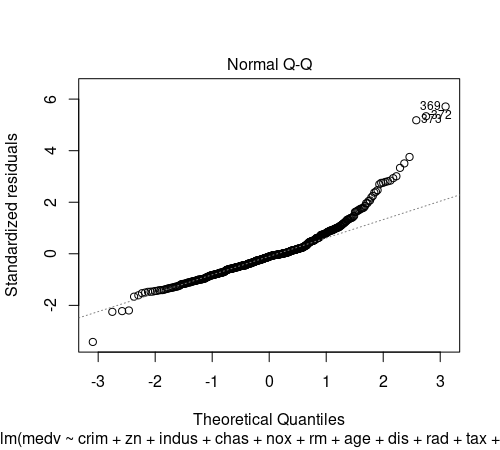
★Q-Qプロット(上記右図)
横軸に標準正規分布の分位点、縦軸に残差の分位点をプロットしています。
正規分布である場合、データ プロットは直線になります。
369、372、373は、残差プロット同様、残差の絶対値が大きく、正規分布から外れている※と考えられます。
※外れ値の除去については検討が必要になります。
以下、参考図書です。Rを最初からきっちり学びたい方にお勧めです。



コメント