「この顧客は、キャンペーンに反応してくれる可能性が高いか?」
「どの特徴を持つ製品が、高い評価を得やすいか?」
前回は、機械学習の代表的な手法として、判断のプロセスが分かりやすい決定木について紹介しました。

決定木は、データを分類するためのルールを木構造で表現するため、なぜその予測結果になったのかを直感的に理解しやすいという大きなメリットがありました。
しかし、決定木には学習データに過剰に適合してしまい、新しいデータに対する予測精度が落ちやすい(過学習)という弱点もあります。
そこで今回は、その弱点を克服し、より高い予測精度を実現する手法であるランダムフォレストについて、Rのコードと共に解説します。
1. ランダムフォレストとは
2. 使用パッケージとデータ
3. Rでランダムフォレストモデルの構築
3-1. パッケージのインストールと読み込み
3-2. 学習データとテストデータへの分割
3-3. ランダムフォレストモデルの構築
4. モデルの性能評価と変数の重要度
4-1. モデルの性能評価
4-2. 変数の重要度の可視化
5. まとめ
1. ランダムフォレストとは
ランダムフォレストは、複数の決定木を組み合わせることで、個々の木の弱点を補い合い、より頑健で精度の高い予測を目指す手法です。
この複数のモデルを組み合わせる考え方をアンサンブル学習と呼び、機械学習の世界で広く使われています。
決定木を「1本の木」とするなら、ランダムフォレストは文字通り「森(Forest)」を作り、集団の知恵で結論を導き出します。1本の木だけではデータの偏りやノイズに影響されて判断を誤ることがあっても、森全体で考えれば、一部の木が間違えても他の多くの木が正しい判断をし、全体として安定した精度の高い予測が可能になります。🌳🌳🌳
💡決定木の判断基準:ジニ不純度
決定木は、「この質問をしたら、データがどれだけキレイに分かれるか?」を基準に枝分かれします。この「キレイさ(混じり気のなさ)」を測る代表的な指標がジニ不純度です。
あるグループが、異なるクラス(例:「Yes」と「No」)のデータでごちゃ混ぜになっている状態を「不純度が高い」と言います。
逆に、グループ内のデータがすべて同じクラス(例:全員「Yes」)であれば「不純度が低い(純粋である)」と言い、ジニ不純度は0になります。
決定木は、このジニ不純度が最も小さくなるような質問(分岐ルール)を学習していきます。
💡ランダムフォレストの「2つのランダム性」
ランダムフォレストは、多様な木々からなる「森」を作るために、決定木を学習させる際に2つの「ランダム性(一手間)」を加えます。
・データのランダム抽出(ブートストラップサンプリング): 元の学習データから、ランダムにデータを復元抽出し(同じデータを何度も選ぶ)、それぞれの決定木に異なるデータセットを与えて学習させます。
・特徴量のランダム選択: 木の分岐点(質問)を作る際に、全ての変数(特徴)からではなく、ランダムに選ばれた一部の変数の中から最適な質問を選びます。
この2つの工夫により、多様性に富んだ木々が育ち、結果として過学習を抑え、汎用性の高いモデルが作られます。
★ランダムフォレストのメリット
・高い予測精度: 一般的に、単体の決定木よりも高い精度が期待できます。
・過学習しにくい: 複数の木で学習するため、データへの過剰な適合が起こりにくいです。
★デメリット
・解釈が難しい: 多数の木を組み合わせるため、決定木のように「なぜこの結果になったか」をシンプルに説明することが困難です(ブラックボックス化しやすい)。
・計算コスト: 多数の木を構築するため、決定木よりも学習に時間がかかります。
2. 使用パッケージとデータ
今回も、決定木の記事と同様に、Pima.trデータセット(MASSパッケージ)を使用します。このデータセットは、アメリカ女性(21歳以上)における糖尿病の有無と健康診断データです。
妊娠回数や血糖値、BMIといった健康診断の測定値から、その人が糖尿病かどうかを予測するランダムフォレストモデルを作ります。
npreg:妊娠回数、glu:血糖値、bp:血圧、skin:皮膚の厚さ、bmi:BMI、ped:糖尿病の家族歴(遺伝的リスク)、age:年齢、type:糖尿病の有無(Yes or No)
# MASSパッケージがインストールされていない場合はインストール
# install.packages("MASS")
library(MASS)
data(Pima.tr)
head(Pima.tr)
# 出力結果 # npreg glu bp skin bmi ped age type # 1 5 86 68 28 30.2 0.364 24 No # 2 7 195 70 33 25.1 0.163 55 Yes # 3 5 77 82 41 35.8 0.156 35 No # 4 0 165 76 43 47.9 0.259 26 No # 5 0 107 60 25 26.4 0.133 23 No # 6 5 97 76 27 35.6 0.378 52 Yes
3. Rでランダムフォレストモデルの構築
Pima.trデータセットを使って、ランダムフォレストモデルを構築します。
3-1. パッケージのインストールと読み込み
必要なパッケージをインストールして読み込みます。
# パッケージがインストールされていない場合はインストール
# install.packages("randomForest")
# install.packages("caret")
library(randomForest)
library(caret)
3-2. 学習データとテストデータへの分割
決定木の時と同様に、データの70%を学習用、30%をテスト用に分割します。学習データでモデルを作成し、テストデータでその精度を検証します。
# 乱数を固定
set.seed(123)
# データを学習用とテスト用に分割 (70%を学習データ、30%をテストデータ)
train_index_pima <- createDataPartition(Pima.tr$type, p = 0.7, list = FALSE)
train_data_pima <- Pima.tr[train_index_pima, ]
test_data_pima <- Pima.tr[-train_index_pima, ]
# 分割結果の確認
print(paste("学習データ数:", nrow(train_data_pima)))
print(paste("テストデータ数:", nrow(test_data_pima)))
# 出力結果 [1] "学習データ数: 141" [1] "テストデータ数: 59"
3-3. ランダムフォレストモデルの構築
学習データを使ってランダムフォレストモデルを構築します。目的変数をtype、それ以外を説明変数として指定する書き方は決定木と同じです。
これから実行するrandomForest()関数の中で、ブートストラップサンプリングが自動的に行われ、指定した数だけ決定木が作成されることで「森」が構築されます。
# 乱数を固定して結果を再現可能にする
set.seed(123)
# ランダムフォレストモデルの構築
# ntree引数で500本の決定木を作成(デフォルトも500)
rf_model_pima <- randomForest(type ~ ., data = train_data_pima, ntree = 500)
# モデルの概要を確認
print(rf_model_pima)
# 出力結果
Call:
randomForest(formula = type ~ ., data = train_data_pima)
Type of random forest: classification
Number of trees: 500
No. of variables tried at each split: 2
OOB estimate of error rate: 30.5%
Confusion matrix:
No Yes class.error
No 75 18 0.1935484
Yes 25 23 0.5208333
出力結果の「OOB estimate of error rate」は Out-of-Bag (OOB) 誤差と呼ばれ、モデル構築時に使用されなかったデータ(各木が学習に使わなかったデータ)を使って内部的に精度を検証した際の誤分類率です。テストデータを使わなくても、モデルのおおよその性能を把握することができます。
作成される木の数はモデルの性能と計算時間に影響します。一般的に、木が多いほど性能は安定しますが、ある一定数を超えると性能向上は頭打ちになり、計算時間だけが増えていきます。
モデルオブジェクトをplot関数で描画すると、木の数を増やしたときのエラー率の推移を確認できます。
# エラー率の推移をプロット
plot(rf_model_pima, main = "木の数とエラー率の関係")
legend("topright", legend=c("OOB", "No", "Yes"), col=c("black", "green", "red"), lty=1:3)
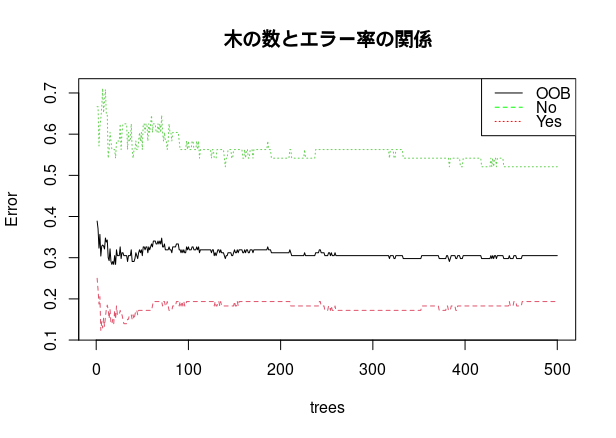
このプロットを見ると、黒い線のOOB(Out-of-Bag)エラー率は、木の数が100本を超えたあたりから安定しています。この場合、計算時間を短縮したければntree = 200程度に設定しても、精度は大きく変わらない可能性が高いと判断できます。
4. モデルの性能評価と変数の重要度
モデルを構築した後は、その性能を客観的に評価し、どのような判断根拠で予測を行っているのかを分析することが重要です。ここでは「モデルの性能評価」と「変数の重要度」の2つの側面からモデルを検証します。
4.1. モデルの性能評価
構築したモデルが未知のデータ(テストデータ)に対してどれだけの予測精度を持つかを確認します。predict()関数でテストデータの予測を行い、confusionMatrix()関数で正解率などの性能指標を確認します。
# テストデータで予測を行う predicted_rf <- predict(rf_model_pima, test_data_pima) # 混同行列を作成して精度を評価 confusionMatrix(data = predicted_rf, reference = test_data_pima$type, positive = "Yes")
# 出力結果
#Confusion Matrix and Statistics
Reference
Prediction No Yes
No 36 9
Yes 3 11
Accuracy : 0.7966
95% CI : (0.6717, 0.8902)
No Information Rate : 0.661
P-Value [Acc > NIR] : 0.01668
Kappa : 0.5104
Mcnemar's Test P-Value : 0.14891
Sensitivity : 0.5500
Specificity : 0.9231
Pos Pred Value : 0.7857
Neg Pred Value : 0.8000
Prevalence : 0.3390
Detection Rate : 0.1864
Detection Prevalence : 0.2373
Balanced Accuracy : 0.7365
'Positive' Class : Yes
テストデータに対する正解率(Accuracy)は約79.7%でした。前回の決定木モデル(約74.6%)と比較して、精度が向上していることが分かります。
4.2. 変数の重要度の可視化
ランダムフォレストは多数の木を組み合わせるため、判断プロセスがブラックボックス化しやすい弱点があります。しかし、「どの変数が予測に重要だったか」を可視化することで、モデルの判断根拠を探る手がかりを得ることができます。
varImpPlot()関数を使い、変数の重要度を「予測精度への貢献度(MeanDecreaseAccuracy)」と「分類の純度への貢献度(MeanDecreaseGini)」の2つの指標で見てみます💡
# 変数の重要度をプロット varImpPlot(rf_model_pima, main = "変数の重要度")
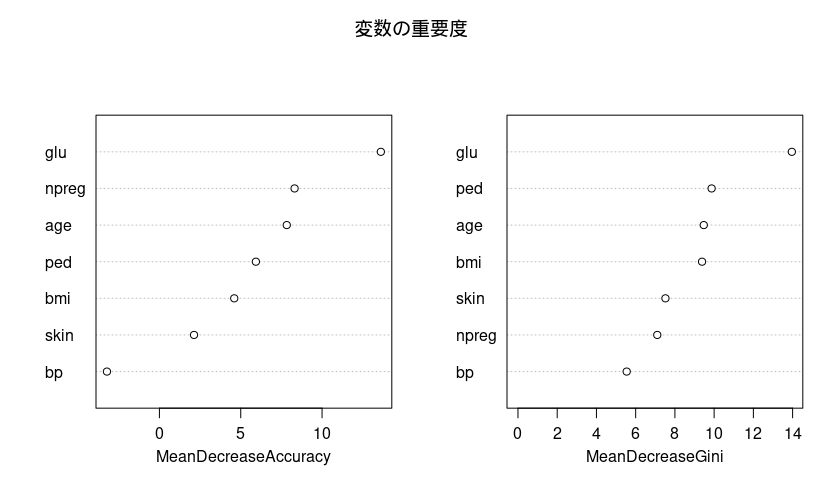
💡プロットの見方
このプロットは、各変数が糖尿病の予測にどれだけ貢献したかを2つの視点から示しています。どちらの図も、右にある(値が大きい)ほど重要度が高いことを意味します。
・MeanDecreaseAccuracy(精度の平均減少量/左図): その変数をモデルから削除すると、モデル全体の正解率がどれだけ低下したかを示します。低下の度合いが大きいほど、予測に不可欠な変数と言えます。
・MeanDecreaseGini(ジニ不純度の平均減少量/右図): その変数が木の分岐に使われるたびに、ジニ不純度が平均してどれだけ減少したかを示します。この値が大きいほど、データを効率よく分類する能力が高いことを意味します。
このモデルは、二つの指標ともにglu(血糖値)が最も分類に貢献していることが分かりました。2番目以降は指標によって順位が異なりました。予測精度の観点ではnpreg(妊娠回数)とage(年齢)が、モデル内部の分類ロジックの観点ではped(家族歴)とage(年齢)が重視される結果でした。
このように、異なる指標を複数用いてモデルを多角的に評価することで、一つの側面だけでは見えてこないモデルの特性を深く理解でき、より信頼性の高い分析に繋がります💡
5. まとめ
今回は、決定木を発展させた強力なアンサンブル学習手法であるランダムフォレストについて、Rでの実装から評価までの一連の流れを解説しました。
複数の木と「2つのランダム性」を組み合わせることで、決定木の弱点であった過学習を抑え、より精度の高い予測モデルを構築できることが大きな魅力です。
その一方で、モデルの解釈は複雑になりますが、変数の重要度を評価することで、どの変数が予測に貢献しているかを多角的に分析できることも確認できました。
決定木とランダムフォレスト、それぞれの長所と短所を理解し、目的に応じて使い分けてみてください。






コメント