まなびの目標🎯
・モンテカルロ法の基本的な考え方を、円周率の計算を例に理解する。
・AIの代表的な学習方法である教師あり学習と教師なし学習の違いを理解する。
・確認テストで学びを復習!
1. ランダムさで答えを探す「モンテカルロ法」
1.1 モンテカルロ法とは
1.2 Pythonで円周率を求めてみよう!
2. AIはどうやって賢くなる?機械学習の仕組み
2.1 教師あり学習:お手本から学ぶ
2.2 教師なし学習:データ自身から学ぶ
2.3 どっちの学習法を使う?
3. まとめ
4. 確認テスト
1. ランダムさで答えを探す「モンテカルロ法」
1.1 モンテカルロ法とは
モンテカルロ法とは、正確な答えを計算するのが難しい問題に対し、コンピュータで乱数(ランダムな数)を大量に発生させたシミュレーション(模擬実験)を繰り返し行い、その結果を統計的に分析することで、近似的な答えを求める手法のことです。
1.2 Pythonで円周率を求めてみよう!
この手法を使って、円周率π(パイ)を計算するシミュレーションをしてみます。
1辺が2の正方形の中に、半径1の円がぴったり入っている図形を考えます。
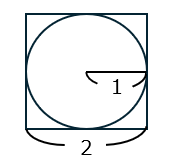
この正方形の中にランダムに点をたくさん打ち、円の中に入った点の割合を数えることで、円周率を近似計算します。
import random
import matplotlib.pyplot as plt
!pip install japanize-matplotlib # 日本語フォントをインストール(Google Colab用)
# pip install japanize-matplotlib # Google Colab以外
import japanize_matplotlib
# 乱数の発生パターンを固定する(シード値を設定)
random.seed(0) # 同じ数字を使い続ける限り同じ乱数が出る
# ① 変数の初期化(準備)
num_trials = 10000 # 試行回数
points_in_circle = 0 # 円の内側に入った点の数
circle_x, circle_y = [], [] # 円の内側の点の座標リスト
outside_x, outside_y = [], [] # 円の外側の点の座標リスト
# ② モンテカルロ法のシミュレーション
for _ in range(num_trials):
# -1から1の範囲でランダムなx, y座標を生成
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
# 原点からの距離の2乗を計算
distance_squared = x**2 + y**2
# 距離の2乗が1以下なら円の中
if distance_squared <= 1:
points_in_circle += 1
circle_x.append(x)
circle_y.append(y)
else: # 円の外
outside_x.append(x)
outside_y.append(y)
# ③ 円周率の推定値を計算
# (円の面積) / (正方形の面積) = (円の中の点の数) / (全ての点の数)
# (1 * 1 * π) / (2 * 2) = points_in_circle / num_trials
# π = 4 * (points_in_circle / num_trials)
pi_estimate = 4 * (points_in_circle / num_trials)
print(f"試行回数: {num_trials}回")
print(f"円周率の推定値: {pi_estimate}")
# ④ 結果をグラフで描画
plt.figure(figsize=(6, 6))
plt.scatter(circle_x, circle_y, color='blue', s=1, label='円の内側')
plt.scatter(outside_x, outside_y, color='red', s=1, label='円の外側')
plt.title(f'モンテカルロ法による円周率の推定 (試行回数: {num_trials}回, π ≈ {pi_estimate:.4f})')
plt.legend()
plt.show()
# 出力結果 試行回数: 10000回 円周率の推定値: 3.1236
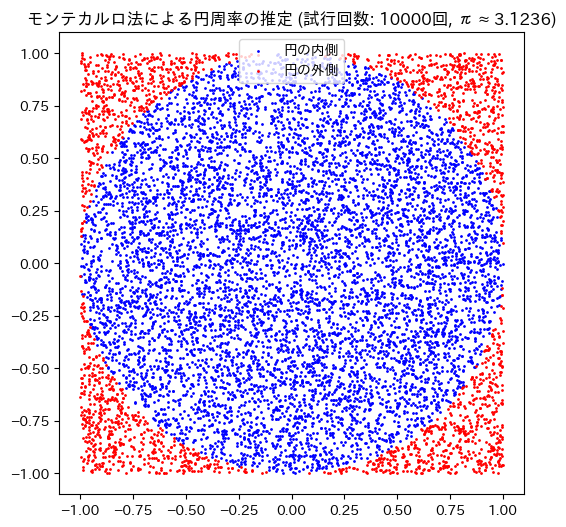
試行回数:1000で、π=3.0720
試行回数:10000で、π=3.1236
試行回数:100000で、π=3.1288
試行回数:1000000で、π=3.1411
試行回数を増やすほど、円周率の真の値(約3.14159…)に近づいていきました。
☕コラム モンテカルロ法とAIの関係
実は、今回学んだモンテカルロ法も、AIの分野(特に強化学習など)で「未来をシミュレーションして最善の手を探す」ために使われています(例:AlphaGo)。 「乱数」と「データ」は、現代のAIを支える重要な要素なのです。 では、その「AI(機械学習)」は具体的にどうやって賢くなるのでしょうか?次章で見ていきましょう。
2. AIはどうやって賢くなる?機械学習の仕組み
AIが賢くなるための学習方法を機械学習と呼びます。 これは、人間が一つ一つのルールを教え込むのではなく、コンピュータが大量のデータの中からパターンや法則を自力で見つけ出す仕組みのことです。
機械学習の例を2つ見ていきます。
2.1 教師あり学習:お手本(正解)から学ぶ
問題と正解がペアになったデータ(お手本)を大量に与え、その関係性のパターンをAIに学習させる方法です。
目的: 新しいデータに対して、正解を予測したり、種類を分類したりすること。
得意なこと:
ー 分類: 画像が「犬」か「猫」か、メールが「迷惑メール」か「通常メール」かを見分ける。
ー 回帰(予測): 過去の気温と売上のデータから、未来の売上を予測する。家の広さや駅からの距離から、その家の価格を予測する。
2.2 教師なし学習:データ自身から学ぶ
正解データを与えず、AIがデータそのものの構造や隠れたパターンを自力で見つけ出す方法です。
目的: データに潜む共通点を見つけてグループ分けしたり、データの構造を要約したりすること。
得意なこと:
ー クラスタリング(グループ分け): ECサイトの顧客の購買履歴から、似たような買い方をする顧客を自動でグループ分けする(例:「健康志向グループ」「特売品好きグループ」など)。
ー 次元削減: データの本質的な特徴を保ったまま、よりシンプルな表現に圧縮する。
2.3 どっちの学習法を使う?
どちらの手法を使うかは、「何がしたいか(目的)」と「どんなデータを持っているか」によって決まります。
・正解を予測したい場合 → 教師あり学習
(例:この画像が犬か猫か知りたい、明日の売上を予測したい)
・データの構造や関係性を知りたい場合 → 教師なし学習
(例:顧客がどんなグループに分かれるか知りたい、データの傾向を掴みたい)
このように、AIは課題に応じて適切な学習方法を使い分けることで、様々な問題を解決しています。
3. まとめ
・モンテカルロ法は、乱数を使ったシミュレーションを繰り返すことで、計算が難しい問題の近似解を得る手法である。
・AIの学習法には、正解データ(お手本)から未来の予測や分類を行う教師あり学習と、正解データなしでデータの構造やグループ分けを発見する教師なし学習がある。
4. 確認テスト
Q1. 正方形の中にランダムに点を打ち、円の中に入った点の割合から円周率を推定するような手法を何と呼びますか?
- 教師あり学習

- モンテカルロ法

- 教師なし学習

![]() 正解!
正解!
![]() 不正解!
不正解!
モンテカルロ法
ヒント:たくさんの偶然の試行から、答えを導き出します。
Q2. 大量の犬の画像に「犬」という正解ラベルを付けてAIに学習させる方法は?
- モンテカルロ法

- 教師なし学習

- 教師あり学習

![]() 正解!
正解!
![]() 不正解!
不正解!
教師あり学習
ヒント:正解の情報がついたデータを用いて学習させる方法です。
Q3. ECサイトが、顧客の購買履歴データだけをAIに分析させて、顧客をいくつかのグループに自動で分類させるのは、主に何と呼ばれますか?
- 回帰

- 分類

- クラスタリング

![]() 正解!
正解!
![]() 不正解!
不正解!
クラスタリング
ヒント:先生がおらず、AIが自分で法則を見つけ出す学習方法で行われる、代表的なグループ分けの手法です。
Q4. 過去の天気とアイスクリームの売上データを使って、明日の天気予報から売上を予測するAIモデルを作る場合、どちらの学習手法が適していますか?
- どちらでもない

- 教師あり学習

- 教師なし学習

![]() 正解!
正解!
![]() 不正解!
不正解!
教師あり学習
ヒント:「明日の売上」という「正解」を予測したい場合です。
確認クイズは、いかがでしたでしょうか?今回の学習内容が、皆さんの情報活用能力を高める一助となれば幸いです。閲覧いただき、ありがとうございました!
※本記事 教科書該当範囲
| 教科書名 | 該当章 |
| 新編情報Ⅰ(東京書籍) | 3章 29. モデル化とシミュレーション |
| 最新情報I(実教出版) | 第5章 3節 1. モデル化とシミュレーション |
| 高校情報ⅠPython(東京書籍) | 第5章 29. モデル化とシミュレーション |
本サイトは、教科書をベースに構成しています。使える「情報Ⅰ」を目指し、毎週新しい記事を発信予定です。



本記事に対し、お気づきの点ございましたらお問い合わせよりご連絡頂けますと幸いです。





コメント