目的変数と複数の説明変数があった場合、目的変数の予測に用いることができるのが重回帰分析です。
重回帰分析を行う際、そのモデルに使用する変数を適切に選択することはとても重要です。
今回使用するデータセットのBostonは、Housing Values in Suburbs of Boston（ボストン近郊の住宅価格）と、1住戸当たりの平均部屋数、町ごとの一人当たり犯罪率、持ち家の値段（中央値）などの14の変数情報が含まれます。
「持ち家の値段を予測するために、他の13の変数情報が全て必要なのか？」
必要な変数で精度が高い重回帰モデルを作る方が、よりよい予測ができるはず💡
そこで行うのが、変数選択（特徴量選択）です。
本記事では、RのBostonデータセットを例に、モデルのあてはまりの良さを表す、AIC（赤池情報量基準）とBIC（ベイズ情報量基準）の値を用いて変数選択を行います。
変数選択の方法には、ステップワイズ法を用い、Rのコードを含めて解説を行います。
1. モデルのあてはまりの良さ（AIC, BIC)
モデルの”あてはまりの良さ“を評価する指標として、AIC（赤池情報量基準） と BIC（ベイズ情報量基準） がよく使われます。
これらの指標は、モデルがデータにどれだけ適合しているかを示し、同時にモデルの複雑さにもペナルティを与えることで、過剰適合を防ぎつつ、シンプルで良いモデルを選択するのに役立ちます。
■AIC（赤池情報量基準）
AIC（Akaike Information Criterion）は、モデルの適合度と複雑さのバランスを評価する指標で、値が小さいほどモデルの予測精度とシンプルさが両立できているとされます。
AICの式：
AIC=−2×log(L)+2×p
L：モデルの尤度（データに対する適合度）で大きいほどデータに適合していることを示す。
p：モデルのパラメータ数（変数数）で、複雑さに応じてペナルティが増加する。
式の前項部分がモデルの適合度を示し、後項部分がモデルの複雑さを示しています。
AICはデータに対する予測精度を重視し、モデルがデータをどれだけうまく説明するかを評価しています。
■BIC（ベイズ情報量基準）
BIC（Bayesian Information Criterion）は、AICと同様にモデルの適合度と複雑さを評価しますが、ペナルティが強く、よりシンプルなモデルを選びやすい特徴があります。
BICの式：
BIC=−2×log(L)+log(n)×p
L：モデルの尤度（データに対する適合度）で大きいほどデータに適合していることを示す。
p：モデルのパラメータ数（変数数）で、複雑さに応じてペナルティが増加する。
n：サンプルサイズを示し、サンプルサイズが大きくなるとペナルティが大きくなる。
BICは、式の後項で変数数が多いほどペナルティが増えることからも、モデルのシンプルさをより重視していることが分かります。適合度とモデルの複雑さのバランスをとりながら、変数選択を行います。
Lの詳細は、こちらを参照ください。
AICとBICについては、以下の論文で議論されています。
Burnham K. P., Anderson D. R. (2004). Multimodel inference understanding AIC and BIC in model selection. Sociological Methods & Research, 33, 261–304.
2. AIC/BICを使ったステップワイズ法による変数選択
ステップワイズ法は、重回帰モデルの変数選択手法の一つで、モデルの適合度を考慮しつつ、不要な変数を含めず、最適なモデルを見つけます。進め方は以下の3つがあります。
前進選択法：変数を一つずつ追加していく方法。
後退削除法：初期段階で全変数を含み、変数を一つずつ削除していく方法。
双方向法：変数の追加と削除を交互に行う柔軟な方法。
各ステップで変数を追加または削除してAICやBICなどの評価指標を最小化する方向に進めます。
今回は、よりよいモデルが得られやすい双方向法を選択します。
ここでは、AICとBICの両方で変数選択行います。
2.1 目的変数以外の全変数を用いたモデルの作成
まずは、Bostonデータセットを使って住宅価格（medv）を予測するため、medv以外の全変数を用いて重回帰モデルを作成します。
2.3 BICを用いたステップワイズ法
次に、BIC基準のステップワイズ法による変数選択を行います。
step_model_BIC <- step(full_model, direction = "both", k = log(nrow(Boston))) #1 ステップワイズ法（双方向法）、BIC #Start: AIC=1648.81 #AIC表示だが、これはBICの値 #medv ~ crim + zn + indus + chas + nox + rm + age + dis + rad + # tax + ptratio + black + lstat # Df Sum of Sq RSS AIC #- age 1 0.06 11079 1642.6 #- indus 1 2.52 11081 1642.7 #<none> 11079 1648.8 #- chas 1 218.97 11298 1652.5 #- tax 1 242.26 11321 1653.5 #- crim 1 243.22 11322 1653.6 #- zn 1 257.49 11336 1654.2 #- black 1 270.63 11349 1654.8 #- rad 1 479.15 11558 1664.0 #- nox 1 487.16 11566 1664.4 #- ptratio 1 1194.23 12273 1694.4 #- dis 1 1232.41 12311 1696.0 #- rm 1 1871.32 12950 1721.6 #- lstat 1 2410.84 13490 1742.2 #Step: AIC=1642.59 #medv ~ crim + zn + indus + chas + nox + rm + dis + rad + tax + # ptratio + black + lstat # Df Sum of Sq RSS AIC #- indus 1 2.52 11081 1636.5 #<none> 11079 1642.6 #- chas 1 219.91 11299 1646.3 #- tax 1 242.24 11321 1647.3 #- crim 1 243.20 11322 1647.3 #- zn 1 260.32 11339 1648.1 #- black 1 272.26 11351 1648.7 #+ age 1 0.06 11079 1648.8 #- rad 1 481.09 11560 1657.9 #- nox 1 520.87 11600 1659.6 #- ptratio 1 1200.23 12279 1688.4 #- dis 1 1352.26 12431 1694.6 #- rm 1 1959.55 13038 1718.8 #- lstat 1 2718.88 13798 1747.4 #Step: AIC=1636.48 #medv ~ crim + zn + chas + nox + rm + dis + rad + tax + ptratio + # black + lstat # Df Sum of Sq RSS AIC #<none> 11081 1636.5 #- chas 1 227.21 11309 1640.5 #- crim 1 245.37 11327 1641.3 #- zn 1 257.82 11339 1641.9 #- black 1 270.82 11352 1642.5 #+ indus 1 2.52 11079 1642.6 #- tax 1 273.62 11355 1642.6 #+ age 1 0.06 11081 1642.7 #- rad 1 500.92 11582 1652.6 #- nox 1 541.91 11623 1654.4 #- ptratio 1 1206.45 12288 1682.5 #- dis 1 1448.94 12530 1692.4 #- rm 1 1963.66 13045 1712.8 #- lstat 1 2723.48 13805 1741.5 summary(step_model_BIC) #Call: #lm(formula = medv ~ crim + zn + chas + nox + rm + dis + rad + # tax + ptratio + black + lstat, data = Boston) #Residuals: # Min 1Q Median 3Q Max #-15.5984 -2.7386 -0.5046 1.7273 26.2373 #Coefficients: # Estimate Std. Error t value Pr(>|t|) #(Intercept) 36.341145 5.067492 7.171 2.73e-12 *** #crim -0.108413 0.032779 -3.307 0.001010 ** #zn 0.045845 0.013523 3.390 0.000754 *** #chas 2.718716 0.854240 3.183 0.001551 ** #nox -17.376023 3.535243 -4.915 1.21e-06 *** #rm 3.801579 0.406316 9.356 < 2e-16 *** #dis -1.492711 0.185731 -8.037 6.84e-15 *** #rad 0.299608 0.063402 4.726 3.00e-06 *** #tax -0.011778 0.003372 -3.493 0.000521 *** #ptratio -0.946525 0.129066 -7.334 9.24e-13 *** #black 0.009291 0.002674 3.475 0.000557 *** #lstat -0.522553 0.047424 -11.019 < 2e-16 *** #--- #Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 #Residual standard error: 4.736 on 494 degrees of freedom #Multiple R-squared: 0.7406, Adjusted R-squared: 0.7348 #F-statistic: 128.2 on 11 and 494 DF, p-value: < 2.2e-16
BIC基準で双方向ステップワイズ法を行い、最適な変数を選択ました。
最初のモデル（全変数を含む）ではBICが1648.81からスタートし、各ステップで変数の増減を試みながらBICを低下させました。
ageやindusなどが削除されることでBICが減少し、最適な組み合わせが選ばれました。
最終的に、ageとindusが除外され、11個の変数が残るモデルが選択され、BICは1636.48に達しました。
今回のデータでは、AICとBICのそれぞれのステップワイズ法によって同じ変数選択を行われたため、回帰係数も一致し、同じモデルが得られました。
3. 最適化モデルのプロット
AICとBICのステップワイズ法で得られた最適化モデル：
lm(formula = medv ~ crim + zn + chas + nox + rm + dis + rad + tax + ptratio + black + lstat, data = Boston)
このモデルについて、実測値と予測値のプロット（青）を行います。
傾き１（実測値＝予測値を示す）の基準線（赤）も合わせて引きます。
library(ggplot2)
predicted_values <- predict(step_model_AIC)
data_plot <- data.frame(Actual = Boston$medv, Predicted = predicted_values)
ggplot(data_plot, aes(x = Actual, y = Predicted)) +
geom_point(color = "blue", alpha = 0.6, size = 2) +
geom_abline(intercept = 0, slope = 1, color = "red", linetype = "dashed", size = 1) + #基準線
labs(title = "実測値-予測値",
x = "実測値",
y = "予測値") +
theme_classic() +
theme(plot.title = element_text(hjust = 0.5)) +
scale_x_continuous(limits = c(0,50)) + # X軸の範囲を設定
scale_y_continuous(limits = c(0, 50)) # Y軸の範囲を設定
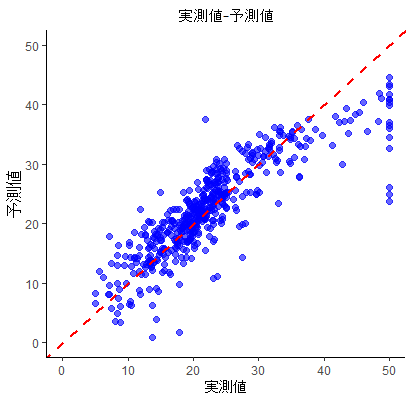
図で見ると、基準線周辺にプロットされていて、実測値に対してよく予測できているようなモデルが作成できました。
今回は、線形の重回帰モデルを作成しましたが、その他にもLasssoやリッジ回帰といった正則化法に基づく回帰分析もありますので、後日紹介したいと思います。
ありがとうございました。
以下のサイトにRでの単回帰分析や重回帰分析について書いていますので、閲覧いただけると幸いです。
参考図書▼▼▼
コメント