カイ二乗検定とは、観察データが期待データとどの程度一致するかを評価する統計手法です。
主に”カテゴリデータ(質的データ)”の分析に用いられます。
1. カイ二乗検定とその使用事例
カイ二乗検定(Chi-square test)とは、カテゴリーデータの分布が期待される分布と一致しているかどうかを検定するための統計手法です。
主に、「観測データが特定の分布に従っているか」、「二つのカテゴリーデータが独立しているか」を調べる際に用いられます。
視覚化にはモザイクプロットなどが用いられることがあります。
◆カイ二乗検定の種類
①適合度検定(Goodness-of-fit test):
観測されたデータが特定の理論分布に適合しているかを調べる。
②独立性の検定(Test of independence):
二つのカテゴリ変数が独立しているかを調べる。
◆各検定の使用事例
①適合度検定の例
・サイコロの公平性の検定


事例: サイコロを60回振った結果が、各面(1から6)が出る回数として10回ずつ出ることが期待される。
検定の使用: 実際の観測結果が期待される分布(各面が10回ずつ出る)にどの程度適合しているかをカイ二乗検定で検証する。
・遺伝の検定
事例: メンデルの遺伝の法則に基づき、ある植物の花の色が特定の比率(例えば3:1の比率)で出現することが期待される。
検定の使用: 実際に観測された花の色の比率が理論的な比率(3:1)にどの程度適合しているかをカイ二乗検定で検証する。
・消費者の購買行動
事例: ある製品が購入される曜日について、全ての曜日で均等に(例えば各曜日14%ずつ)購入されることが期待される。
検定の使用: 実際の観測結果が期待される分布(各曜日14%ずつ)にどの程度適合しているかをカイ二乗検定で検証する。
②独立性の検定の例
・医療データの解析
事例: 異なる治療法Aと治療法Bの効果を比較する際、治療効果があるかどうかを調べる。
使用: 治療効果の有無に関するデータを解析する。治療法Aと治療法Bを受けた患者の中で、効果があった患者と効果がなかった患者の比率が異なるかどうかを検定する。

・顧客満足度調査
事例: 新製品の顧客満足度が既存製品と異なるかどうかを調べる。
使用: 新製品と既存製品の顧客満足度の評価(満足、不満足)を比較し、顧客の評価が異なるかどうかを検定する。
・教育データの解析
事例: 異なる教育プログラムが学生の成績に与える影響を評価する。
使用: 異なるプログラムを受けた学生の成績(合格、不合格)の分布を比較し、教育プログラムが成績に与える影響があるかどうかを検定する。
カイ二乗検定はさまざまな分野で活用されており、適切に使用することで、データに基づいた意思決定をサポートします。
では、カイ二乗検定の①適合度検定と②独立性の検定のそれぞれの手順を解説したいと思います。
2. Rでの適合度検定の手順
対立仮説(H1): 観測データは期待される分布に従っていない。
2. 観測データの収集:実際に観測されたデータを収集する。
3. 期待度数の計算: 理論分布に基づいて、各カテゴリに期待される度数を計算する。
4. カイ二乗値の計算: 観測度数と期待度数の差を平方し、期待度数で割った値を合計してカイ二乗値を算出する。
5. 有意性の検定: カイ二乗値をカイ二乗分布と比較して、有意性を判断する。

observed <- c(60, 40) # 観測データ
expected <- c(50, 50) # 期待度数(均等に分布する場合)
chi_square_test <- chisq.test(observed, p = expected/sum(expected)) # カイ二乗統計量の計算
print(chi_square_test) # 1 結果の表示
# Chi-squared test for given probabilities
# data: observed
# X-squared = 4, df = 1, p-value = 0.0455 # カイ二乗統計量、自由度、p値
検定結果・結論:
適合度検定の結果、カイ二乗値は4、自由度1、p値は0.0455でした。
有意水準を0.05とした場合、p値 < 0.05であるので、帰無仮説を棄却し、対立仮説を支持します。
つまり、コインの表と裏の出現回数に統計学的に有意な差があると言えます。
この例題では、観測された度数分布は期待される度数分布に適合していないことが分かりました。
適合度検定を使用することで、観測データが期待される理論分布にどれだけ近いかを評価することができます。
3. Rでの独立性の検定の手順
◆独立性の検定の手順
1. 仮説の設定:
帰無仮説(H0): 2つの変数は独立である。
対立仮説(H1): 2つの変数は独立でない(関連がある)。
2. データの収集:
2つのカテゴリカル変数のデータを収集し、クロス集計表を作成する。
3. 期待度数の計算:
ある仮説のもとで(例えば、行と列の因子はそれぞれ独立であると仮定した場合に)期待される数値(期待度数)を求める。
各セルの期待度数の計算:
期待度数=E = \( \frac{\text{行の合計} \times \text{列の合計}}{\text{全体の合計}} \)
期待度数は、各行と列の合計から求める。
4. カイ二乗値の計算
カイ二乗値の計算:
カイ二乗値 = \( \chi^2 = \sum \frac{(\text{O} – \text{E})^2}{\text{E}} \)
(O:観測度数、E:期待度数)
5. 結果の解釈:
計算したカイ二乗値を自由度に基づいてp値と比較し、帰無仮説を棄却するかどうかを判断する。
◆データセットでの検定例を解説
例題:新しい治療法Aと従来の治療法Bの効果有り無しの数を収集した。治療法Aは、効果あり30件と効果なし20件、治療法Bは効果あり25件と効果なし25件であった。この結果が互いに独立の関係であるといえるか。
仮説:帰無仮説(H0): 新しい治療法Aと従来の治療法Bの効果は互いに独立である。
対立仮説(H1): 新しい治療法Aと従来の治療法Bの効果は互いに独立でない。
この仮説に基づいて、独立性の検定(カイ二乗検定)を行います。
Rでのデータセット作成コードは以下の通りです。
observed_1 <- matrix(c(30, 20, 25, 25), nrow=2, byrow=TRUE)
colnames(observed_1) <- c("効果あり", "効果なし")
rownames(observed_1) <- c("A", "B")
observed_1
# 効果あり 効果なし
#A 30 20
#B 25 25
chi_sq_test <- chisq.test(observed, correct = F) # カイ二乗検定の実行 イェーツの補正なし(デフォルトが補正有)
> print(chi_sq_test)
Pearson's Chi-squared test
data: observed
X-squared = 1.0101, df = 1, p-value = 0.3149
検定結果・結論:
カイ二乗検定の結果、カイ二乗値は1.0101、自由度1、p値は 0.3149でした。
有意水準を0.05とした場合、p値 < 0.05であるので、帰無仮説を棄却することはできません。
従って、新しい治療法Aと従来の治療法Bの効果は互いに独立しており、治療法Aと治療法Bの効果には統計的に有意な関連は見られないことが示されました。
※Yates(イェーツ)の補正
カイ2乗検定は、以下の前提とされています。※1、2(これらも、諸説あります)
(1) データが母集団から無作為に抽出されている
(2) サンプル・サイズが十分に大きい。小さな標本にカイ2乗検定を適用すると、タイプIIの過誤(帰無仮説が実際には偽であるにもかかわらず、帰無仮説を受け入れること)のリスクがある。
(3)期待度数Eの1/5以上が5より小さくなく、クロス集計表のカウントがゼロのセルがない。
これらに該当しない場合に用いられる補正方法の一つが、イェーツの補正です。
chi_sq_test_1 <- chisq.test(observed_1, correct = TRUE) # カイ二乗検定の実行 イェーツの補正を適用
> print(chi_sq_test_1)
# Pearson's Chi-squared test with Yates' continuity correction
#data: observed_1
#X-squared = 0.64646, df = 1, p-value = 0.4214
ただし、イェーツの補正は過剰補正になりがちであるという意見もあり※3、上記(1)~(3)を満たさない場合は、補正を行うのではなく別の方法を推奨する意見もあります。
こちらの補正方法を使用の場合は、充分に検討の上、ご使用ください。
※2 Bolboacă, S.D., Jäntschi, L., Sestraş, A.F., Sestraş, R.E., Pamfil, D.C. (2011). Pearson-Fisher Chi-Square statistic Revisited. Information. 2(3):528-545. https://doi.org/10.3390/info2030528
※3 Onchiri S, Conceptual model on application of chi-square test in education and social sciences. Educational Research and Reviews 2013. doi: 10.5897/ERR11.0305
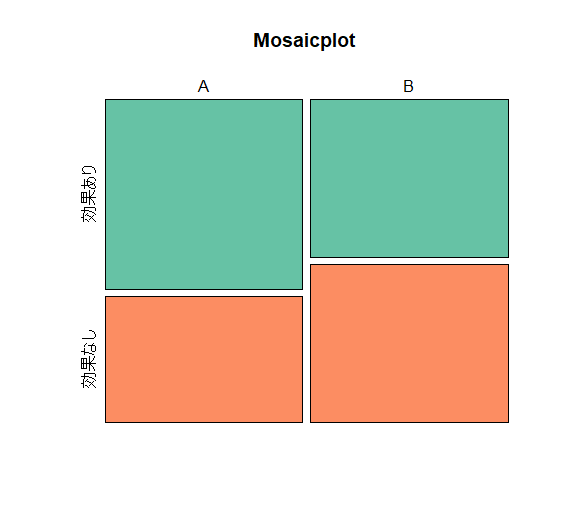
4. Rによるデータの可視化(モザイクプロット)
モザイクプロットは、カテゴリカルデータの関係や分布を視覚的に表現するグラフです。
2次元のクロス集計表を基に作成され、各セルの面積が観測度数に比例し、色分けされることが特徴です。
モザイクプロットは複数のカテゴリや多層的なデータの比較に役立ち、視覚的な理解を深めるのに有効です。
observed_table <- as.table(observed_1)
mosaicplot(observed_table, col = RColorBrewer::brewer.pal(3, "Set2"), main = "Mosaicplot",cex.axis = 1) #モザイクプロット
参考:https://www.rdocumentation.org/packages/graphics/versions/3.6.2/topics/mosaicplot
量的データの比較で使用されるt検定などの記事も挙げていますので、ご参考にしていただけると幸いです。
-160x90.png)
t-160x90.png)




コメント