研究や調査を行う前に、適切なサンプルサイズを計算しておくことは、研究や調査の信頼性を確保し、効率よく実施するためにとても重要です。
本記事では、サンプルサイズの計算のうち、仮説検定でのサンプルサイズ決定についてRのコード例と共に紹介したいと思います。
1. サンプルサイズの計算
2. 仮説検定におけるサンプルサイズ決定(検出力、有意水準、効果量を用いた分析)②の特徴
3. 臨床試験における2群検定
4. 製品質量の品質管理
5. サンプルサイズを可視化ー検出力との関係ー
1. サンプルサイズの計算
サンプルサイズの計算には、主に2種類の計算方法があります。
①区間推定におけるサンプルサイズ決定(標準偏差、誤差の許容範囲、信頼水準)
この方法は、母集団の平均や割合などのパラメータを推定する際に使用されます。標準偏差や許容誤差を考慮して、推定の精度を保証するためにサンプルサイズを計算します。アンケート調査や疫学研究など、推定が主目的の試験で多く用いられます。
以前に投稿していますので、ご確認いただけると幸いです。

② 仮説検定におけるサンプルサイズ決定(検出力、有意水準、効果量を用いた分析)
この方法は、統計的仮説検定※1に基づいてグループ間の差や効果の有無を検証する際に使用されます。サンプルサイズ、効果量、検出力を組み合わせて、仮説検定で真の効果をどれだけの確率で検出できるかを評価する手法です。特に、臨床試験や介入研究、実験研究などで頻繁に用いられ、効果を正確に検出するために必要なサンプルサイズの算出が重要です。
本記事では②を紹介したいと思います。
※1 統計的仮説検定
統計的仮説検定は、データを分析して、ある仮説(帰無仮説)が正しいかどうかを判断する方法です。例えば、「差がない」とする帰無仮説を立て、その仮説が正しいと仮定した場合に、得られたデータがどれくらい起こりうるかを調べます。データから、その差が非常に大きく、偶然だけでは説明できないと判断できる場合、帰無仮説(差がないという仮説)を棄却し、対立仮説(差があるという仮説)を支持するという結論に至ります。
2. 仮説検定におけるサンプルサイズ決定(検出力、有意水準、効果量を用いた分析)②の特徴
仮説検定におけるサンプルサイズを決定する際、検出力、有意水準、効果量は非常に重要です。これらの要素を適切に設定することで、信頼性のある試験結果が得られます。
検出力(1 – β):
検出力は、実際に効果が存在する場合に、その効果を正しく検出する確率を示します。
通常、0.8(80%)以上が目標とされ、20%の確率で真の効果を見逃す可能性があることを意味します。
検出力が高いほど、βエラー(見逃しの誤り)が少なくなります。
有意水準(α):
有意水準は、帰無仮説が正しい場合に、それを誤って棄却する確率を表します。
一般的に0.05(5%)に設定されることが多いですが、分野や研究の目的に応じて適した値を選びます。
例えば、αが0.05であれば、5%の確率で誤った差があると判断する可能性があります。
効果量:
効果量は、検定対象の差を定量化した尺度であり、通常Cohenのdなどで表されます。
Cohenのdは、効果量を示す指標の一つで、2つのグループ間の平均の差を標準偏差で割って計算します。
d = (Mean1 – Mean2)/ 標準偏差
この値により、差の大きさが小、中、大のいずれかに分類され、効果の強さを評価できます。一般的には、0.2が小、0.5が中、0.8以上が大きな効果とされます。
3. 臨床試験における2群検定
新薬の血圧低下への効果を調べる臨床試験を設計したいとします。コントロール群と治療群の平均血圧の比較を行う際のサンプルサイズを設定する例を紹介します。

治療によって平均血圧が5 mmHg低下することを期待し、標準偏差は10 mmHgであると仮定し検定力を80%、有意水準を5%に設定し、必要なサンプルサイズを計算します。
平均血圧の差: 5 mmHg
標準偏差: 10 mmHg
検定力(1-β): 80%
有意水準: 5%
上記のような場合でも、一般的に使用される”両側検定”での計算を進めます。
“平均血圧が低下することを期待し”、とありますが、臨床試験に至るまでに新薬によって血圧が低下することがある程度根拠がある場合でも、一般的には、低下する方向の検定、つまり片側検定を行うことは多くないようです。
低下が予測できたとしても、その根拠が科学的に、公に、認められていなければ、両側検定を行うことが推奨される場合が多いです。片側検定は、両側検定に比べて、有意でない差を有意と判断してしまうリスクが高まり、必要なサンプルサイズも小さく見積もられることがあるため、計画段階から十分な注意が必要です。
・帰無仮説 (H₀): 治療によって血圧に変化はない
・対立仮説 (H₁): 治療によって血圧に変化がある(低下または上昇)
# pwrライブラリのインストール・読み込み
# install.packages("pwr")
library(pwr)
# パラメータ設定
mean_diff <- 5 # 期待される平均の差(治療群と対照群の血圧差)
std_dev <- 10 # 標準偏差
alpha <- 0.05 # 有意水準
power <- 0.8 # 検出力
# 効果量(Cohen's d)の計算
effect_size <- mean_diff / std_dev
# サンプルサイズの計算 (両側検定)
result <- pwr.t.test(d = effect_size, sig.level = alpha, power = power, type = "two.sample")
# 結果の表示
print(result)
# Two-sample t test power calculation
# n = 63.76561
# d = 0.5
# sig.level = 0.05
# power = 0.8
# alternative = two.sided
#NOTE: n is number in *each* group
n=63.76561、両側検定で、治療群と対照群の間の効果を検出するために必要なサンプルサイズです。サンプルサイズは少なくとも64人(各群に64人ずつ)が必要であることを示しています。
4. 製品質量の品質管理
ある製品の平均質量が100gであることを目標とし、製造過程で製品の質量にばらつきが生じるため、製品の品質管理を行いたいとします。製品の質量が目標から±5gの範囲に収まっているかを検証するために、両側検定を使ってサンプルサイズを決定します。
期待される重量の差: ±5 g(100gから±5gずれることを許容)
標準偏差: 5 g
有意水準: 5%
検出力: 80%
・帰無仮説 (H₀): 製品の質量には許容範囲を超えるばらつきがある
・対立仮説 (H₁): 製品の質量は許容範囲内(ばらつきがない、または少ない)
library(pwr)
# パラメータ設定
mean_diff <- 5 # 期待される質量の差(±5g)
std_dev <- 5 # 製品質量の標準偏差
alpha <- 0.05 # 有意水準
power <- 0.8 # 検出力
# 効果量(Cohen's d)の計算
effect_size <- mean_diff / std_dev
# サンプルサイズの計算 (両側検定)
result <- pwr.t.test(d = effect_size, sig.level = alpha, power = power,
type = "two.sample", alternative = "two.sided")
# 結果の表示
print(result)
# Two-sample t test power calculation
#n = 16.71472
#d = 1
#sig.level = 0.05
#power = 0.8
#alternative = two.sided
#NOTE: n is number in *each* group ※2
n=16.71472、両側検定で、製品の質量が目標から±5gの範囲に収まっているかを検出するために必要なサンプルサイズです。この場合、サンプルサイズは少なくとも17個のサンプルが必要です。
※2 この場合は、製品1群のばらつきを調べるための検定となるため、サンプルサイズ17は1群についてのことです。この計算は2群比較ではなく、製品の質量のばらつきが目標値からどれだけずれるかを確認する目的で行っています。
5. サンプルサイズを可視化ー検出力との関係ー
4. 製品質量の品質管理の条件で、異なるサンプルサイズに対する検出力を可視化するものです。
サンプルサイズが増えるにつれて、検出力がどのように変化するかがわかります。
library(pwr)
library(ggplot2)
# パラメータ設定
mean_diff <- 5 # 期待される質量の差(±5g)
std_dev <- 5 # 製品質量の標準偏差
alpha <- 0.05 # 有意水準
power <- 0.8 # 検出力
# 効果量(Cohen's d)の計算
effect_size <- mean_diff / std_dev
# 検出力分析のためのサンプルサイズのリスト
sample_sizes <- seq(5, 50, by = 1) # 5から50までのサンプルサイズ
# 各サンプルサイズに対する検出力を計算
powers <- sapply(sample_sizes, function(n) {
result <- pwr.t.test(n = n, d = effect_size, sig.level = alpha, type = "two.sample", alternative = "two.sided")
return(result$power)
})
# データフレームに整理
data_power <- data.frame(Sample_Size = sample_sizes, Power = powers)
# サンプルサイズと検出力の関係を可視化
ggplot(data_power, aes(x = Sample_Size, y = Power)) +
geom_line(color = "green", size = 1) +
geom_point(color = "blue", size = 3) +
theme_minimal() +
labs(title = "Sample Size vs Power",
x = "Sample Size",
y = "Power") +
theme(plot.title = element_text(hjust = 0.5)) +
geom_hline(yintercept = 0.8, linetype = "dashed", color = "red") +
annotate("text", x = 30, y = 0.82, label = "Power = 0.8", color = "red")
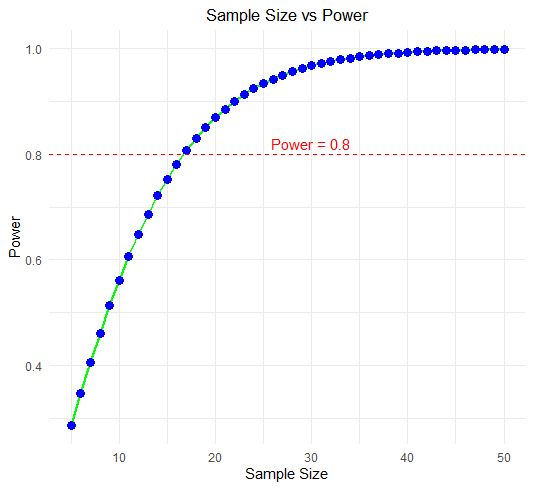
適切なサンプルサイズの計算は、研究の信頼性を高め、無駄なリソースを削減する上で重要です。サンプルサイズの計算において参考にしていただければ幸いです。
「Rでサンプルサイズの計算 ①区間推定」の記事もご参考にしていただければと思います。




コメント