Rでサンプルサイズの計算　①区間推定

5.　アンケート調査のためのサンプルサイズの計算例

ある企業が顧客満足度を調査し、調査結果の平均満足度を±0.1の誤差範囲内で推定したいとします。過去の調査では、満足度の標準偏差は0.3であると推定されています。信頼水準を95%に設定し、必要なサンプルサイズを計算します。

・顧客満足度の標準偏差　σ = 0.3
・許容誤差　E = 0.1
・95%信頼水準　Z = 1.96

サンプルサイズ計算式：
n = (Z ⋅ σ / E)²

# パラメータ設定
sigma2 <- 0.3     # 顧客満足度の標準偏差
E2 <- 0.1         # 許容誤差（±0.1）
Z2 <- 1.96        # 信頼水準95%に対応するZ値

# サンプルサイズの計算
n2 <- (Z2 * sigma2 / E2)^2
n2
#[1] 34.5744

この市場調査の例では、顧客満足度の標準偏差が0.3、許容誤差が±0.1、信頼水準95%という条件で、サンプルサイズが35であることが計算されました。サンプルサイズは、調査結果が指定した精度で推定できるために必要な数を示します。この計算により、信頼性のある推定を行うために必要な最小限のサンプル数を事前に算出することが可能です。

6.　サンプルサイズを可視化ー許容誤差を変化させてみるー

5.　アンケート調査のためのサンプルサイズの計算例での、顧客満足度の標準偏差を0.3、信頼水準を95%に固定し、許容誤差を変化させた場合のサンプルサイズの変化をグラフで示します。

library(ggplot2)
# パラメータ設定
sigma <- 0.3        # 顧客満足度の標準偏差
Z <- 1.96           # 信頼水準95%に対応するZ値
# 許容誤差の範囲を設定
errors <- seq(0.01, 0.5, by = 0.01)
# 許容誤差に対するサンプルサイズを計算
sample_sizes <- (Z * sigma / errors)^2
# データフレームにまとめる
data <- data.frame(errors = errors, sample_sizes = ceiling(sample_sizes))
data
#   errors sample_sizes
#1    0.01         3458
#2    0.02          865
#3    0.03          385
#4    0.04          217
#5    0.05          139
#6    0.06           97
#7    0.07           71
#8    0.08           55
#9    0.09           43
#10   0.10           35
#11   0.11           29　・・・
# サンプルサイズの可視化
ggplot(data, aes(x = errors, y = sample_sizes)) +
geom_line(color = "blue", size = 1.2) +
labs(title = "許容誤差とサンプルサイズの関係",
x = "許容誤差",
y = "必要なサンプルサイズ") +
theme_classic()　#図

許容誤差が小さくなるほどサンプルサイズ数は多く必要になります。
例えば、許容誤差が0.1の場合は、サンプルサイズ35で、許容誤差が0.05の場合はサンプルサイズ139です。

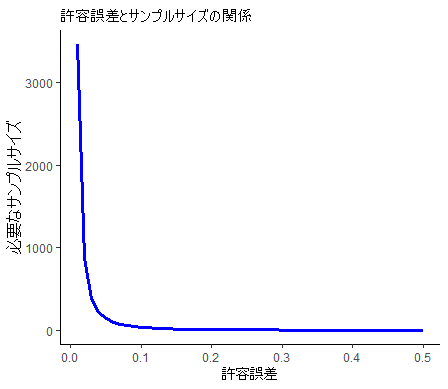
可視化によって、より理解しやすくなりました。

② 仮説検定におけるサンプルサイズ決定（検出力、有意水準、効果量を用いた分析）についても、後日解説記事を作成予定です。

他にも、Rでの解析や可視化に関するコード例を含む記事をあげていますので、ご参考にしていただけると幸いです。

Rでデータ解析と可視化

Rを用いたデータ解析や可視化方法について、コード例を含めた解説記事を投稿しています。

hira-labo.com