例えば、同じ人が睡眠薬AとBを服用すると、それぞれの効果に差があるのか?ないのか?を知りたいとします。

その際に、よく使用されるのが対応のある2群のt検定です。
”対応のある”2群のt検定は、比べるデータは同じ人がAを服用した場合とBを服用した場合のように、比較する個体は同じ場合で、状況が異なる場合に使用します。
例えば、睡眠薬AとBの服用による差を見る場合でも、同じ人ではなく、別の人がそれぞれAとBを服用して差があるかを検証する場合は、対応のない2群のt検定を行います。
対応のないt検定については以下をご参照ください。
-160x90.png)
t-160x90.png)
まずは、t 検定はどうやって行うのか?を解説していきます。
最後に、t 検定から何が言えるようになるのか?を実際作図を行い、その図を用いてプレゼンテーション形式で表したいと思います。
1.t検定とは
t検定とは、帰無仮説をたて、それを検証する統計的仮説検定です。
以下のような手順で行われます。
「帰無仮説」を立てる:
「帰無仮説」とは統計的仮説検定の際に立てる仮説のこと。帰無仮説を棄却することにより対立仮説を結論とします。
例えば、帰無仮説「2群の平均値に統計学的有意差がない」とします。
⇒有意水準を設定する:
帰無仮説において、おこりうる誤り(第一種の過誤)の基準であり、有意水準は一般的には5%とすることが多く、1%とすることもあります。
p値が有意水準以下になると、帰無仮説は棄却され、対立仮説が結論となります。
⇒t値、p値を算出:
(x‾:データの平均、μ:母平均、s 2:不偏分散、n:サンプルサイズ)
t = (x––μ)/√s2/n
t値が決まると、t分布表からp値を算出することができます。 ※これらの計算はRでできますので御参考程度で。
⇒p値と有意水準を比較し、帰無仮説について結論を出す:
p値と有意水準を比較し、p値<=有意水準 となれば、帰無仮説が棄却され、対立仮説を結論とします。
p値>有意水準 となれば、帰無仮説は棄却されません。
上記のように、帰無仮説「2群の平均値に統計学的有意差がない」とした場合、
有意水準1%とした場合、p値<=0.01であれば、帰無仮説は棄却され、「2群に統計学的有意差がある」と結論付けることができます。
p値>0.01であれば、帰無仮説は棄却出来ませんが、決して「2群に差がない」の証明はできないので、「2群の平均値に統計学的有意差があるとは言えない」と結論づけます。
このように、p値を算出し、有意水準と比較することで、統計学的有意差について述べることができます。
2. 対応のある2群のt検定とは?
◆データセット
sleep 学生の睡眠データ(以下の#1を参照)
10人の患者に対して、2種類(group1, 2)の睡眠薬の効果(extra:コントロールに対する睡眠時間の増加量)を示したデータです
同じIDは、同じ人物を意味します。
sleep #1データの中身を表示
extra group ID
1 0.7 1 1
2 -1.6 1 2
3 -0.2 1 3
4 -1.2 1 4
5 -0.1 1 5
6 3.4 1 6
7 3.7 1 7
8 0.8 1 8
9 0.0 1 9
10 2.0 1 10
11 1.9 2 1
12 0.8 2 2
13 1.1 2 3
14 0.1 2 4
15 -0.1 2 5
16 4.4 2 6
17 5.5 2 7
18 1.6 2 8
19 4.6 2 9
20 3.4 2 10
with(sleep,t.test(extra[group == 1],extra[group == 2],paired = TRUE)) #2 group1とgroup2を対応あるデータとしてt検定
Paired t-test
data: extra[group == 1] and extra[group == 2]
t = -4.0621, df = 9, p-value = 0.002833 #3 t値とp値
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.4598858 -0.7001142
sample estimates:
mean of the differences
-1.58
#2で対応あるデータのt検定を実施します。ここでは対応ある2群の検定なので、paired=TRUE を記載します。
#3にt値とp値の算出結果が出てきます。 t 値=-4.0621, p 値=0.002833
先ほど1.で説明した「帰無仮説」として、「2群に差がない」を設定し、有意水準1%にて帰無仮説について検証します。
p値が0.28%であるため、有意水準1%をp値が下回った(p<=0.01)ので、「2群に差がない」という帰無仮説は棄却されました。
ですので、対立仮説である「2群に統計学的有意差がある」が結論となりました。
ただし、あくまでも統計的な検定において、帰無仮説に対して有意水準を設定し、それに対してどうであるかの結論であることをご理解頂けたらと思います。
なお、有意水準については批判もあるので、こちらを一読されると良いかと思います。
3. Rで箱ひげ図 ーp値 アスタリスク表示ありー
では、次に「対応のある2群」の t 検定結果をRで箱ひげ図で表してみます。
この度使用するパッケージは”ggpubr”です。この中にggplot2も含まれているので、基本的にはggplot2での作業に近いコードが使えます。
installされていない方は、”ggpubr”をinstallしてからlibraryで使えるようにしてから作業をして下さい。
library(ggpubr)
ggpaired(data = sleep, x = "group", y = "extra", xlab = "group", ylab = "extra") +
stat_compare_means(comparisons = list(c("1", "2")),method = "t.test", paired=TRUE) #4
ggpaired(data = sleep, x = "group", y = "extra", color="group", line.color = "gray",xlab = "group", ylab = "extra") +
stat_compare_means(comparisons = list(c("1", "2")), label = "p.signif", method = "t.test", paired=TRUE)+ylim(-2,7.5) #5
#4 で表示されたのが下の図です。
group1と2の対応するデータを線で繋いで表示されます。
stat_compare_means(comparisons = list(c(“1”, “2”)),method = “t.test”, paired=TRUE) では、
comparisonsでgroupの”1″と”2″を比較するようlistを、method=”t. test”でt検定を、paired=TRUEで対応あるデータであることを、それぞれ指定しています。
p値表示は、デフォルトで値=0.0028 を表示しています。
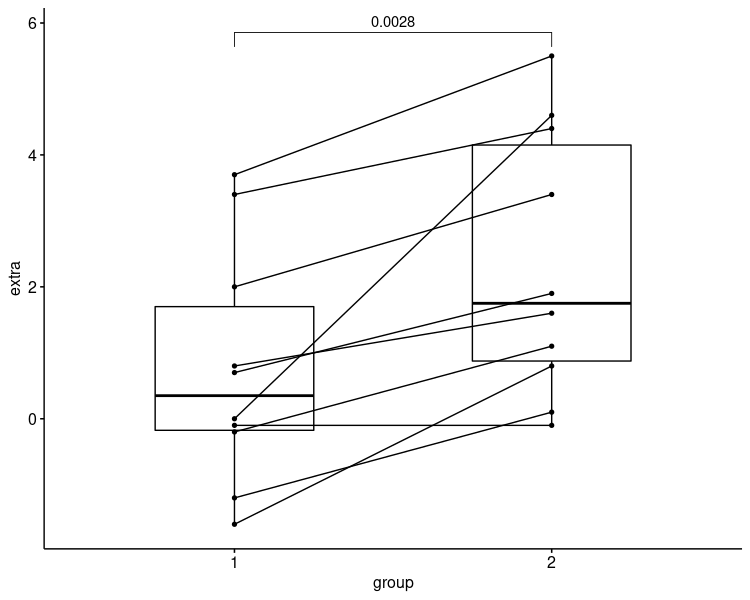
箱ひげ図だけだと、平均値が近く、差が小さいように見えますが、
対応する2群、つまり同一人物の薬剤1と薬剤2の結果を線でつなぐことで、ほとんどのデータがgroup1より2の方が数値が上がっていることがわかります。
#5 もう少し色を使って見やすく、かつp値ではなくアスタリスク*で、表示をしてみます。
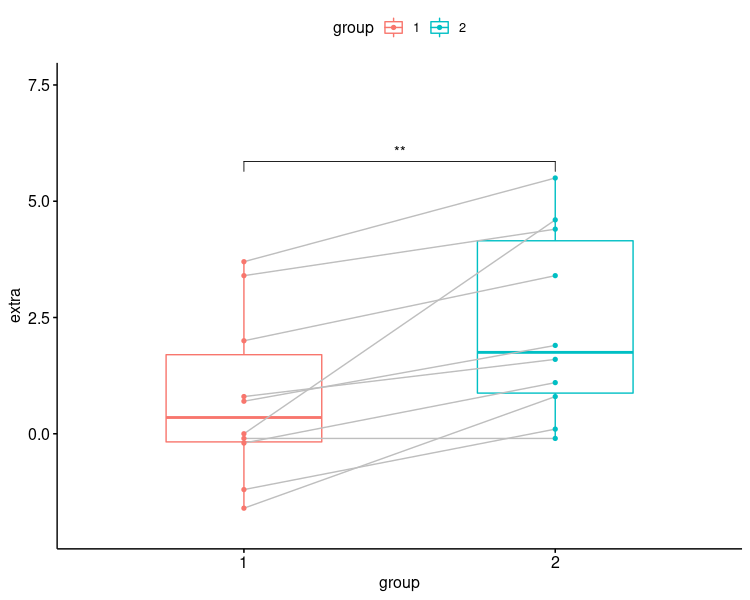
group1と2を ggpaired( , color=”group”, )を入れることで、色わけを行いました。それに伴い凡例も表示されました。
line.color = “gray”, を入れて、対応するデータ同士の線を薄くしてみやすくしました。
有意水準をアスタリスクで表示するため、stat_compare_means( ,label = “p.signif”, )としました。
なお、アスタリスクは、ns: p > 0.05, *: p <= 0.05, **p <= 0.01, ***p <= 0.001 とされており、p値に応じて表示が異なります。
最後に +ylim(-2,7.5)で表示するy軸の幅を設定すると、よりアスタリスクの表示が見やすくなりました。
では、次にこの図を用いたプレゼン資料を作成してみます。
4. Rでプレゼンテーション ー箱ひげ図を使ってー
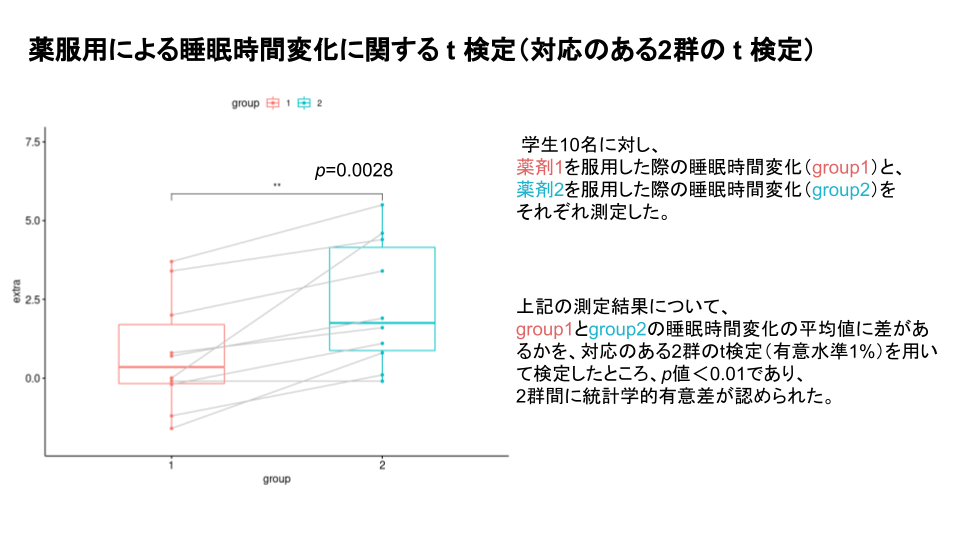

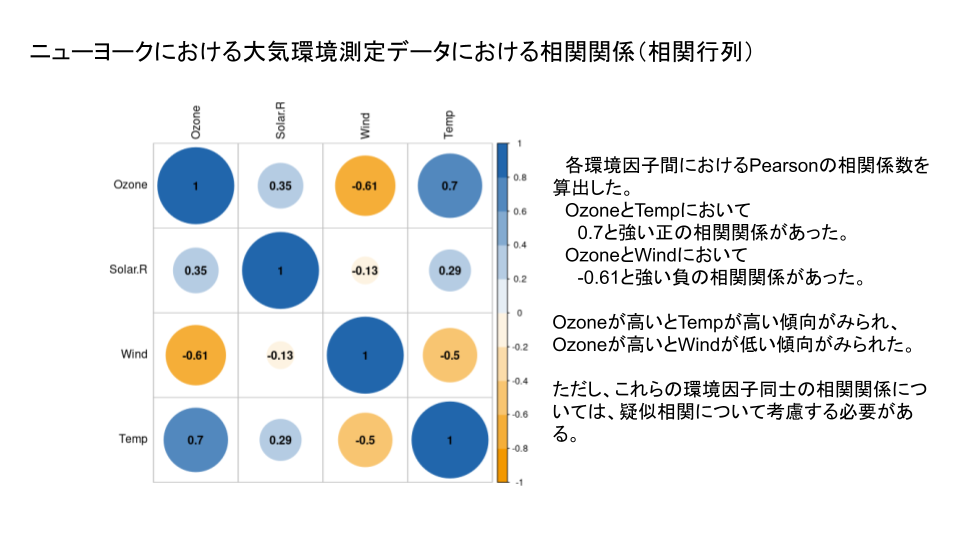
コメント