アンケート調査や臨床試験、観察研究などで、欠損値があるデータはよく見られます。
データを解析する前に、欠損値の適切な処理を行うことはとても重要です。
そのために、データの欠損メカニズムを理解し、適した処理方法を選択していく必要があります。
※参考 欠損のメカニズム（↓↓以下サイト参照）
・完全にランダムな欠損値（MCAR：missing completely at random）：欠損値が、欠損自体を含む変数や他の観測された変数などと関係なくランダムに発生する場合。
・ランダムな欠損値（MAR：missing at random）：欠損値が、他の観測された変数に依存するが、他の変数を統制したときに、その変数とは関係なくランダムに発生する場合。
・ランダムでない欠損値（MNAR：missing not at random）：欠損値が、欠損を含む変数のみに依存する、あるいは他の観測されていない変数に依存する場合。
欠損値の処理方法の種類や、その選択の仕方などを、Rのコード例も含めて解説しますので、参考にしていただければ幸いです。
1. 欠損値の処理方法（削除と補完）
欠損値の処理方法には、削除や補完、モデル分析などがあります。
削除：
欠損値を含む行や列を削除するリストワイズ除去法（欠損値が含まれている行全体を削除する）やペアワイズ除去法（欠損値がないペアのみで相関行列などの計算を行う）などが該当します。
実装が簡単ですが、欠損値が多いとデータが大幅に減少し、情報の喪失が大きくなる可能性があります。
例えば、リストワイズ除去法は、MCAR、欠損率が小さい、サンプルサイズが十分大きいなどの場合に使用されますが、それ以外は、欠損値処理後の解析の精度に影響もあるため、あまり推奨されないようです。
補完：
欠損値を他のデータから推測する方法です。例えば、単一代入法（平均値代入法、確定的回帰代入法など）、多重代入法などが該当します。
データ全体のサンプル数を維持しながら、欠損を補うことができるため、分析の精度を確保しやすくなります。
ただし、補完方法によっては、データに偏りが生じ、分析結果の精度が低下する可能性があります。
例えば、平均値代入法は、MCAR、欠損率が小さい、変数の分散が小さい、データの外観を把握する初期の処理などで使用されることがあります。
一般的なデータにおいては、分散が小さくなるなど、その後の解析の精度に影響が懸念されるため、あまり推奨されないようです。
欠損値の削除のリストワイズ除去法、補完の平均値代入法は、以下のサイトでRでの処理方法を解説しています。
今回は、欠損値の補完について解説していきます。
2. 欠損値の補完（単一代入法と多重代入法）
欠損値の補完については、単一代入法と多重代入法などがあります。
単一代入法：
欠損値に対して一つの推定値を使用して補完する方法です。
たとえば、欠損値をその変数の平均値で置き換える平均値代入法や、他の変数を使って回帰モデルを構築し、予測値で補完する確定的回帰代入法があります。
これらの方法は簡単で計算負荷も低いため、データの概要の検証や把握に適しています。
ただ、単一の推定値で補完するため、データのばらつきや不確実性が反映されないなどの課題もあります。
多重代入法：
欠損値を複数の異なる値で複数回補完し、複数のデータセットを生成する方法です。
この方法では、各データセットに対して同じ解析を行い、結果を統合するそのため、欠損値に対する不確実性を反映することができ、分析の精度を向上させます。
多重代入法は計算負荷が高く、分析プロセスが複雑になることがありますが、特に欠損率が高い場合や、より正確な結果が求められる場合に役立ちます。
今回は、MARのダミーデータを作って、補完方法についてみていきたいと思います。
3. MARダミーデータ作成・可視化・検定
MARデータは、欠損値を含む変数に対して、依存関係のある他の変数で、欠損値を補完を行う手法が研究されています。
Xは全データ存在する変数、YはXに依存する欠損値を含む変数とするdataを作成します。
# ランダムデータの生成
set.seed(123) # 再現性のためのシード設定
n <- 100
data <- data.frame(
X = rnorm(n, mean = 50, sd = 10), # 欠損値なしの変数 X 、rnorm() 正規分布に従う乱数作成の関数、mean= 平均、sd= 標準偏差指定
Y = rnorm(n, mean = 100, sd = 15) # 欠損ありの変数 Y
)
# Yに欠損を発生させる（Xの値に依存するMARの設定）
data$Y <- ifelse(data$X > 50 & runif(n) < 0.3, NA, data$Y) # 変数 X の値が50以上の場合、変数 Y に30%の確率で欠損を発生
summary(data) # 欠損の確認
# X Y
#Min. :26.91 Min. : 74.98
#1st Qu.:45.06 1st Qu.: 90.22
#Median :50.62 Median : 96.77
#Mean :50.90 Mean : 99.36
#3rd Qu.:56.92 3rd Qu.:106.77
#Max. :71.87 Max. :148.62
# NA's :19
YにはNAが19個含まれていることが確認できました。
つぎに、作成したデータについて、MARであるかを検定するLittleのMCAR検定を行います。
こちらの検定は、帰無仮説「欠損はMCARである」、対立仮説「欠損はMCARではない」として検定を行います。
p値が有意水準を下まわった場合、帰無仮説が棄却され、MCARではないといえます。
この場合、欠損が他の変数や観測値と関連する可能性があり、MARまたはMNARの可能性が考えられます。
install.packages("naniar")
library(naniar)
data_df <- as.data.frame(data) #データフレームの型に変更
mcar_test(data_df)
# A tibble: 1 x 4
# statistic df p.value missing.patterns
# <dbl> <dbl> <dbl> <int>
#1 16.9 1 0.0000397 2
statistic(統計検定量)、df（自由度）、p.value(p値)、missing.patterns(欠測パターン数)を示します。
p値＜0.05であり、帰無仮説が棄却され、対立仮説が支持されました。
作成したダミーデータは、MCARではなく、MARあるいはMNARの可能性があるといえます。
なお、MARとMNARの区別は困難であり、この結果をもってMARを前提として解析へと進みます。
今回は、単一代入法として、確定的回帰代入法と確率的回帰代入法についてRのコードと共に解説します。
4. 確定的回帰代入法と欠損値補完
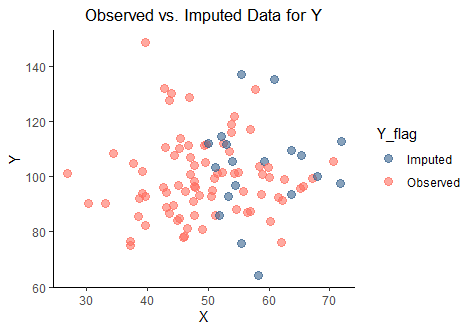
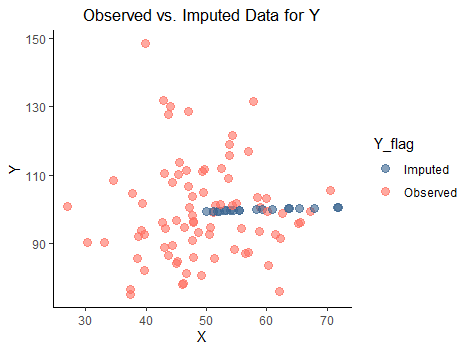
一つの値を補完するため、データのばらつきや不確実性が反映されず、補完後のデータの分散が過小評価される傾向があります。
補完精度よりもシンプルさが求められる場合に適しています。
欠損値がある変数に対して、他の変数を用いた回帰モデルを構築し、補完を行います。
install.packages("mice")
library(mice)
imputed_data <- mice(data, method = "norm.predict", m = 1, maxit=1)
completed_data <- complete(imputed_data)
method = “norm.predict”は確定的回帰代入法を指定
m= は生成する補完データセット数。今回は単一代入法なのでm=1。m>1は多重代入。
maxit= は、補完データセット作成における繰り返し回数。maxit>1は反復代入。
どのように欠損値に補完されたのかをプロットで確認します。
library(ggplot2) library(dplyr) completed_data <- completed_data %>% mutate( Y_flag = ifelse(is.na(data$Y), "Imputed", "Observed") # 元データのYの欠損を参照 ) head(completed_data1) # X Y Y_flag #1 44.39524 89.34390 Observed #2 47.69823 103.85326 Observed #3 65.58708 96.29962 Observed #4 50.70508 94.78686 Observed #5 51.29288 85.72572 Observed #6 67.15065 99.32458 Observed ggplot(completed_data, aes(x = X, y = Y, color = Y_flag)) + geom_point(size = 3, alpha = 0.6) + #size= プロットサイズ、alpha= 色の透明度指定 labs(title = "Observed vs. Imputed Data for Y", x = "X", y = "Y") + scale_color_manual(values = c("Observed" = "#FF6F61", "Imputed" = "#39648f")) + #プロットの色指定 theme_classic()+ theme(plot.title = element_text(hjust = 0.5) #タイトルを中央に寄せた )
確定的回帰代入法で補完された欠損値は、単回帰モデルによる予測値が使用されているため、プロット上で直線的に並んでいることが確認されました。
5. 確率的回帰代入法による欠損値補填
回帰モデルで得られる予測値にランダムな誤差を追加して補完を行います。
この方法は、不確実性の要素を含む1つの補完を行うため、単一の確定的な補足よりも現実的なデータのばらつきを反映しやすくなります。
imputed_data1 <- mice(data, method = "norm.nob", m = 1,maxit=1, set.seed=123)
# iter imp variable
# 1 1 Y
completed_data1 <- complete(imputed_data1)
ggplot(completed_data1, aes(x = X, y = Y, color = Y_flag)) +
+ geom_point(size = 3, alpha = 0.6) +
+ labs(title = "Observed vs. Imputed Data for Y", x = "X", y = "Y") +
+ scale_color_manual(values = c("Observed" = "#FF6F61", "Imputed" = "#39648f")) +
+ theme_classic()+
+ theme(plot.title = element_text(hjust = 0.5)
+ )method = “norm.nob”は確率的回帰代入法を指定
m= は生成する補完データセット数。今回は単一代入法なのでm=1。m>1は多重代入。
maxit= は、補完データセット作成における繰り返し回数。
確率的回帰代入法は、単回帰モデルでの予測値にランダムな誤差も追加されているため、確定的回帰代入法より、よりばらついた値が補完されたことが分かりました。
上記のように、単一代入法については精度などの課題もあり、多重代入法などが推奨される場合もあります。
多重代入法については、後日投稿予定です。
その他、Rでの統計解析や可視化について記事をあげていますので、参考にしていただけると幸いです。
Rを用いたデータ解析や可視化方法について、コード例を含めた解説記事を投稿しています。
参考図書▼▼▼
コメント