Rで欠損処理①　ーna.omit, is.na, na.rm, 欠損値含むダミーデータ作成、リストワイズ除去法、平均値代入法ー

データ解析を行うデータを確認すると、データの抜け、いわゆる「欠損値」を含むことがあります。
データに欠損値があると、データの解析やモデリングが適切に行えないことも多く、データの前処理が必要になります。
この記事では、Rでの欠損値の処理方法について解説します。

■目次
1. 欠損のメカニズム
2. 欠損値を含むダミーデータ作成・欠損パターンの可視化
3. 欠損値の削除（na.omit, リストワイズ除去法）
4. 欠損値の補完（is.na, na.rm, 平均値代入法の紹介）

1. 欠損のメカニズム

データに欠損値がある場合、その欠損値がどのようなメカニズムで生じたのかを理解することは、データ分析の精度や信頼性において非常に重要です。
欠損値が生じるメカニズムについて、3つの異なるタイプに分類されています。

・完全にランダムな欠損値（MCAR：missing completely at random）：欠損値が、欠損自体を含む変数や他の観測された変数などと関係なくランダムに発生する場合。
・ランダムな欠損値（MAR：missing at random）：欠損値が、他の観測された変数に依存するが、他の変数を統制したときに、その変数とは関係なくランダムに発生する場合。
・ランダムでない欠損値（MNAR：missing not at random）：欠損値が、欠損を含む変数のみに依存する、あるいは他の観測されていない変数に依存する場合。

実際、MCARの確認には、LittleのMCAR検定を用いて検証されることもあります。
また、MARとMNARの区別は、観測データから明確に区別することが難しいため、実際の欠損を含むデータについてはMARを前提として次の処理工程へ進むことも多いようです。

2. 欠損値を含むダミーデータ作成・欠損パターンの可視化

欠損値の処理方法を確認していくために、欠損値を含むダミーデータを作成してみます。
今回は、完全にランダムな欠損値を含むMCARのデータを作成します。

set.seed(123) # 乱数のシードを設定
n <- 100 # データの行数
p <- 5 # データの列数
data <- matrix(rnorm(n * p), ncol = p) # 標準正規分布からの乱数によるダミーデータの生成
#　　 　　　 [,1]　　　　 [,2] 　　　　　[,3]　　　  　 [,4] 　　　　　[,5]
#[1,] -0.56047565 　-0.71040656　 2.1988103　 -0.7152422 　-0.07355602
#[2,] -0.23017749　 0.25688371 　1.3124130　 -0.7526890 　-1.16865142
#[3,] 1.55870831 　-0.24669188　 -0.2651451　 -0.9385387 　-0.63474826
#[4,] 0.07050839　 -0.34754260　  0.5431941　 -1.0525133　 -0.02884155
#[5,] 0.12928774　 -0.95161857　 -0.4143399　 -0.4371595　 0.67069597
#[6,] 1.71506499 　-0.04502772　 -0.4762469　 0.3311792 　-1.65054654

missing_prop <- 0.1　 # 欠損値の割合 10%と指定
missing_index <- sample(1:(n*p), size = round(n*p*missing_prop)) # 欠損値が入るインデックスの選択（ランダム）
data[missing_index] <- NA　 # 欠損値を設定
head(data)　#5列×100行のデータ　6行目まで表示
#　 　　　[,1] 　　　　　　[,2] 　　　　　[,3]　　　　 [,4]　　　　　 [,5]
#[1,] -0.56047565　 -0.71040656　 2.1988103　 -0.7152422 　-0.07355602
#[2,] -0.23017749　 0.25688371　 1.3124130　 -0.7526890　 -1.16865142
#[3,] 1.55870831　 -0.24669188　 -0.2651451　 -0.9385387　 -0.63474826
#[4,] 0.07050839 　-0.34754260　 0.5431941 　-1.0525133 　-0.02884155
#[5,] 0.12928774　 -0.95161857　 -0.4143399　 -0.4371595 　 0.67069597
#[6,] 1.71506499 　-0.04502772　　　　   NA    　　　　NA 　-1.65054654

欠損値をランダムにいれたdataが生成され、head(data)を確認すると、NA(欠損値)が入っていることが確認できました。

作成したデータの欠損パターンを確認します。

install.packages("VIM")　#Rで欠損データの可視化と分析を行うためのパッケージ
library(VIM)　　
aggr(data, col = c("#FF6F61", "#708090"), numbers = TRUE, sortVars = TRUE,
      labels = names(data), cex.axis = .8, gap = 3, ylab = c("Missing data", "Pattern"))　 #1　欠損パターンを可視化
# Variables sorted by number of missings: 
# Variable Count
#       V1  0.14
#       V4  0.14
#       V3  0.11
#       V5  0.06
#       V2  0.05

#1　col = c(“#FF6F61”, “#708090”) ⇒色指定、
numbers = TRUE ⇒欠損パターンの割合表記、
sortVars = TRUE⇒欠損値の多い割合順に並べる、
labels = names(data) ⇒各変数ラベルにdataの変数名を使用、
cex.axis= 軸ラベルサイズ、gap= ⇒棒グラフ間のスペース指定、ylab= y軸ラベル指定

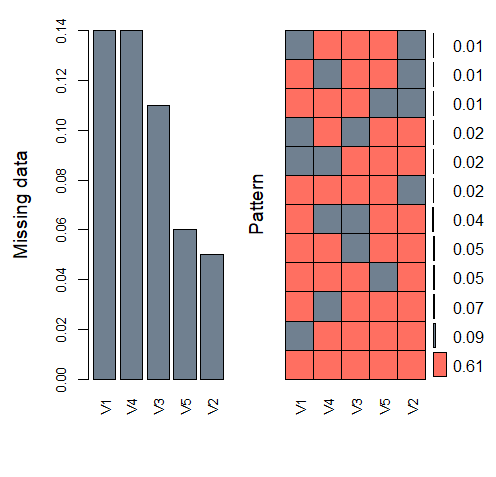
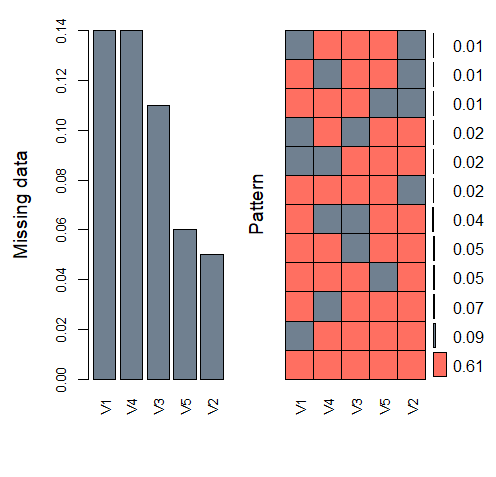
左の棒グラフは、欠損値が含まれる割合を示しており、V1とV4は全体の14％が、V2は5％でした。
右は欠損パターンを示しており、グレーが欠損値、コーラルピンクが観測値を示します。
右端のスケールは、各パターンの全体に対する割合を示しており、
例えば一番下のパターンは、いずれの変数においても欠損値がないものを示し、そのパターンの割合が全体の61％であることを示します。

MCARの場合、欠損値データを削除する方法（リストワイズ除去法など）や、欠損値に各変数の平均を補完する方法（平均値代入法）などを使用することがあります。

作成したダミーデータを使用して、リストワイズ除去法と平均値代入法を紹介していきます。
なお、これらを用いる際の注意点なども記載していますので、ご確認のうえ、ご使用ください。

3. 欠損値の削除（na.omit, リストワイズ除去法）

欠損値を含む行を削除する方法である「リストワイズ除去法」の手順を解説していきます。

data1<- na.omit(data) # 欠損値を含む行を削除
head(data1)　 #5列×61行のデータに（列：ncol(data1)と行：nrow(data1)で確認）
#      　　　 [,1] 　　　　　[,2] 　　　　[,3]　　　　　 [,4] 　　　　　[,5]
#[1,] -0.56047565　 -0.7104066　 2.1988103　 -0.7152422　 -0.07355602
#[2,] -0.23017749　  0.2568837　 1.3124130 　-0.7526890 　-1.16865142
#[3,] 1.55870831 　 -0.2466919 　-0.2651451　 -0.9385387 　-0.63474826
#[4,] 0.07050839　  -0.3475426 　 0.5431941　 -1.0525133　 -0.02884155
#[5,] 0.12928774 　 -0.9516186　 -0.4143399 　-0.4371595 　0.67069597
#[6,] 0.46091621 　 -0.7849045 　-0.7886028 　-2.0142105    -0.34975424

欠損値を含む行が削除できましたので、このデータを用いて、続きの解析を進めることができます。

これは最も簡単な欠損値の処理方法ですが、欠損がある行を全て除去するため、場合によってはデータが大幅に減少し、データの有益な情報を失う可能性があります。
本ダミーデータは、全データの1割が欠損値ですが、欠損値を含む行を削除すると、61%までに削除され、大幅にサンプルサイズが小さくなっています。

リストワイズ除去法は、欠損データがMCARである、欠損率が少ない、サンプルサイズが十分に大きいなど、処理をしても分析結果への影響が十分に小さい場合の処理方法として使われることがあるようです。
選択される際は慎重にご検討されてください。

4. 欠損値の補完（is.na, na.rm, 平均値代入法の紹介）

平均値代入法は、欠損値に、変数（列）の平均値を代入する方法です。
平均値代入法は、欠損値に対し1つの決まった値を補完するため、単一代入法と呼ばれます。

for (i in 1:ncol(data)) {　　　　　　　　　　　
  col_mean <- mean(data[, i], na.rm = TRUE)  #1 列の平均値を計算、na.rm=TRUEで欠損値を無視
  data[is.na(data[, i]), i] <- col_mean     # is.naで欠損値を平均値で置き換え
}
head(data)
         　　   [,1]      　　　  [,2]    　　　　   [,3]     　　　   [,4]     　　　   [,5]
[1,] -0.56047565　 -0.71040656 　 2.1988103 　-0.71524219　 -0.07355602
[2,] -0.23017749 　 0.25688371 　 1.3124130　 -0.75268897 　-1.16865142
[3,]  1.55870831　 -0.24669188 　-0.2651451 　-0.93853870　 -0.63474826
[4,]  0.07050839 　-0.34754260　  0.5431941　 -1.05251328 　-0.02884155
[5,]  0.12928774 　-0.95161857　 -0.4143399　 -0.43715953　  0.67069597
[6,]  1.71506499 　-0.04502772 　 0.1683519　 -0.08064404 　-1.65054654

#1　na.rm=TRUEで欠損値を無視するというコード。欠損値があるとmeanの計算できないため。

欠損値を平均値で補完すると、データの変動を反映しない一律の値で補完するため、データの分散が過小評価される傾向があります。
これにより、標準偏差や相関係数の推定も低く見積もられ、分析結果の精度が低くなります。

他にも、単一代入法（確定的回帰代入法など）や多重代入法などの欠損値補完方法も使用されることがあります。
欠損値の処理について、以下に投稿していますので、参考にしていただけたらと思います。