2つの独立した変数をもつ場合の3群以上の比較では、二元配置分散分析を用います。
同時に、その2つの独立変数における交互作用も評価します。
3群以上の比較で、分散分析の一元配置分散分析(one-way ANOVA)を紹介しました。
上記の記事の一元配置分散分析では、3群間で1つの変数を比較しました。
1. 二元配置分散分析(two-way ANOVA)とその使用事例
二元配置分散分析(two-way ANOVA)は、2つの異なる要因が結果に与える影響を同時に評価するための統計的手法です。
◆二元配置分散分析の使用事例
・異なる教育法(例えば、対面教育とオンライン教育)と生徒の性別(男性、女性)が成績に与える影響を調べる
・異なる治療法(例えば、薬物治療とリハビリ治療)と年齢層(若年層、中年層、高齢層)が健康指標(例えば、血圧、心拍数)に与える影響を調べる
・異なる肥料(有機肥料、化学肥料)と水やりの方法(点滴灌漑、スプリンクラー灌漑)が植物の成長(例えば、身長、葉数)に与える影響を調べる など
2. 二元配置分散分析(箱ひげ図、主効果と交互作用)
二元配置分散分析は、以下の手順で実行されます。
以下、帰無仮説とし、二元配置分散分析で検証します。
・独立変数Aの平均には差がない(主効果の確認)
・独立変数Bの平均には差がない(主効果の確認)
・独立変数AとBの間には交互作用はない(交互作用の確認)
今回は、農業における肥料(treatment 独立変数A)と水やりの方法(irrigation 独立変数B)が農産物の収穫量(weight)に与える影響を調べるコード例を紹介します。
※主効果とは
独立変数が従属変数に与える個別の影響をいいます。
※交互作用とは
二つ以上の独立変数が一緒に従属変数に影響を与えるとき、その影響が単純に個別の影響を足し合わせたものではなく、互いに影響を及ぼし合うことをいいます。例えば、二つの独立変数(因子)の組み合わせで初めて現れる特別な効果(相乗効果など)や、互いの影響を打ち消し合う効果(相殺効果)も交互作用です。
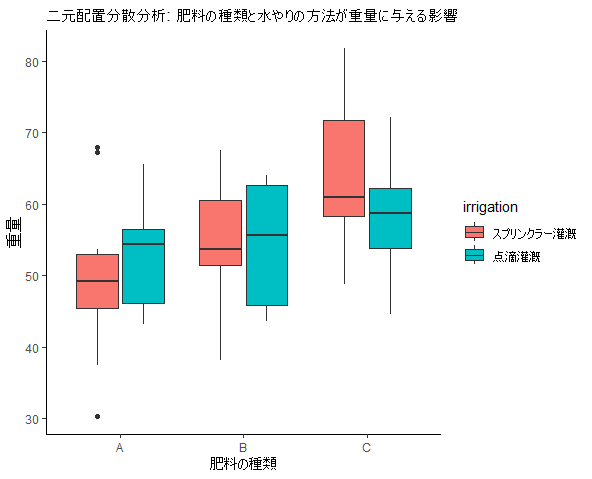
library("ggplot2") set.seed(123) data <- data.frame( #ダミーデータ作成 weight = c(rnorm(20, mean = 50, sd = 10), rnorm(20, mean = 55, sd = 10), rnorm(20, mean = 60, sd = 10)), #rnorm 正規分布の平均が50、標準偏差が10の分布から20個の乱数を生成します。この部分は、最初のグループのデータを表しています。 treatment = factor(rep(c("A", "B", "C"), each = 20)), irrigation = factor(rep(c("点滴灌漑", "スプリンクラー灌漑"), times = 30)) ) model <- aov(weight ~ treatment * irrigation, data = data1) #二元配置分散分析 summary(model) # Df Sum Sq Mean Sq F value Pr(>F) #treatment 2 972 486.0 5.68 0.00577 ** #肥料 #irrigation 1 10 10.3 0.12 0.73014 #水やり #treatment:irrigation 2 217 108.7 1.27 0.28896 #肥料*水やり #Residuals 54 4620 85.6 #--- #Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 ggplot(data1, aes(x = treatment, y = weight, fill = irrigation)) + geom_boxplot() + theme_classic() + labs(title = "二元配置分散分析: 肥料の種類と水やりの方法が重量に与える影響", x = "肥料の種類", y = "重量")
二元配置分散分析の結果、
・肥料の違いによって、重量の平均に統計学的に有意な差がある
・水やりの方法によって、重量の平均に統計学的に有意な差がない
・肥料と水やりの方法の間に交互作用はない
ことが分かった。
3. 交互作用のプロット(可視化)
二元配置分散分析では、各独立変数による主効果だけでなく、独立変数間の交互作用も評価されます。
交互作用を視覚的に捉えるために、作図をしてみます。
library("ggpubr")
ggline(data1, x = "treatment", y = "weight", color = "irrigation", #交互作用
linetype = "irrigation", shape = "irrigation",
add = c("mean_se", "point")) +
labs( x = "肥料の種類", y = "重量")
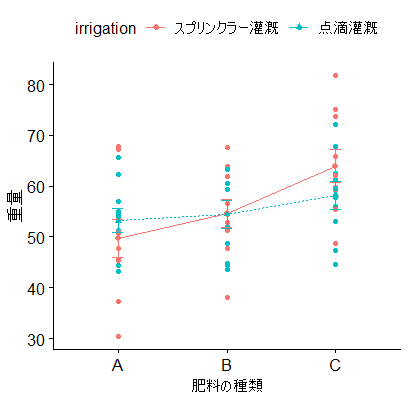
異なる2種類の水やりの方法の線が平行であれば、交互作用がないといえます。
この図は、平行には見えないため、肥料の種類と水やりの方法の間に有意な交互作用がある可能性が考えられました。
しかしながら、二元配置分散分析では、treatment:irrigationのp値は 0.28896であり、統計学的な有意差はない結果でした。
肥料の種類と水やりの方法の間には交互作用がある可能性が視覚的には示唆されましたが、二元配置分散分析の結果、交互作用項のp値が0.289であり、統計的には有意ではないため、交互作用がないと結論づけることができました。
他にも、Rでのデータ解析や可視化の記事を投稿しておりますので、参考にして下さると幸いです。

Rを用いたデータ解析や可視化方法について、コード例を含めた解説記事を投稿しています。


コメント