車の運転速度が速いほど、ブレーキを踏んでから停止するまでに必要な距離は長くなる💡
これは日常の運転でも実感できる事象かと思います。
このような関係性をデータから数式で表現し、予測に活用できる手法である単回帰分析です。
この記事では、車の運転速度を使って、ブレーキを踏んでから停止するまでの距離を予測する単回帰分析の例を紹介します。
単回帰分析は、線形単回帰分析とも呼ばれ、一つの説明変数(ここでは運転速度)から一つの目的変数(停止距離)を予測します。
データセットのcarsを使用し、Rでの分析に必要な手順を解説しながら進めていきます。
1. 単回帰分析とは
単回帰分析は、一つの変数x(説明変数)により一つの変数y(目的変数)を説明・予測する方法です。
説明変数 (独立変数, 予測変数) x: 説明する変数(予測のもととなる変数)
目的変数 (応答変数, 従属変数, 被説明変数) y: 説明される変数(予測される変数)
yi=β0+β1xi+εi (i=1,2,3,…,n)
βは回帰係数で、β0は切片、β1は傾きを表し、εiは誤差項(測定に伴う誤差などを表すもの)です。
車の運転速度(説明変数)を使って、ブレーキを踏んでから停止するまでの距離(目的変数)を予測します。
2. 単回帰分析を行う前に、データの関連性を確認(散布図、相関係数)
今回はcarsのデータセットを使用して、コードを解説します。
carsは、Speed and Stopping Distances of Cars(車の速度と停止距離)のデータです(1920年代)。
単回帰分析を行う前に、データについて散布図や相関係数を確認し、その関係性を把握することは重要です。
散布図を作成し、説明変数と目的変数の間に直線的な関係があることが確認された場合、単回帰分析を適用する価値があると考えられます。
また、相関係数は変数間の関連性の強さを示します。単回帰分析は、一定程度の相関が前提となるため、相関係数の確認は重要です。
head(cars) # carsのデータセット確認
# speed dist #speed(速度), dist(距離)
# 1 4 2
# 2 4 10
# 3 7 4
# 4 7 22
# 5 8 16
# 6 9 10
plot(cars) #1 散布図
cor(cars) #2 相関係数
# speed dist
# speed 1.0000000 0.8068949
# dist 0.8068949 1.0000000
#1 変数間の関連を確認し、右肩上がりのプロット(下図)であることが分かりました。
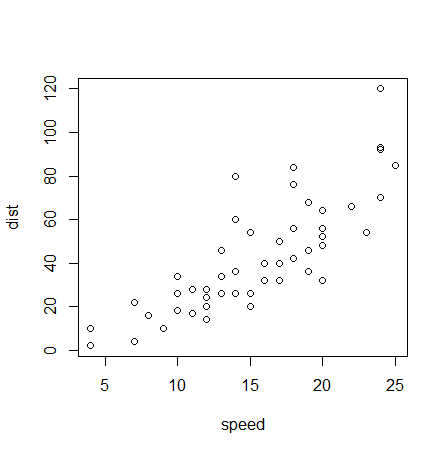
#2 相関係数は0.81であり、これらの変数間には強い正の相関があることが分かりました。
3. 単回帰分析を実施
cars_lm <- lm(dist~speed, data=cars) #3 単回帰分析
plot(dist~speed, data=cars) #4 散布図
abline(cars_lm) #5 単回帰直線を引く
coef(cars_lm) #6 β0とβ1の算出
# (Intercept) speed
# -17.579095 3.932409
summary(cars_lm) #7 単回帰分析の結果の詳細
# Call:
# lm(formula = dist ~ speed, data = cars)
# Residuals:
# Min 1Q Median 3Q Max
# -29.069 -9.525 -2.272 9.215 43.201
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) -17.5791 6.7584 -2.601 0.0123 *
# speed 3.9324 0.4155 9.464 1.49e-12 ***
# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# Residual standard error: 15.38 on 48 degrees of freedom
# Multiple R-squared: 0.6511, Adjusted R-squared: 0.6438
# F-statistic: 89.57 on 1 and 48 DF, p-value: 1.49e-12
#色・軸ラベルをリバイス+回帰式を表示
intercept <- round(coef(cars_lm)[1], 2) #切片 小数点2桁表示
slope <- round(coef(cars_lm)[2], 2) #傾き 小数点2桁表示
regression_eq <- paste0("y = ", slope, "x", intercept) #8 回帰式の表示を作成
regression_eq
# [1] "y = 3.93x-17.58"
library(ggplot2)
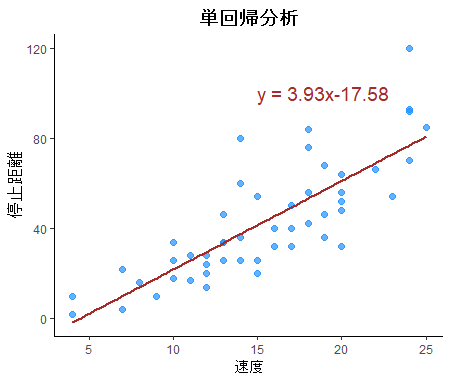
ggplot(data = cars, aes(x = speed, y = dist)) + #9 可視化
geom_point(color = "dodgerblue", size = 2, alpha = 0.7) +
geom_smooth(method = "lm", color = "brown", se = FALSE) +
labs(
title = "単回帰分析",
x = "速度",
y = "停止距離"
) +
theme_classic() +
theme(
plot.title = element_text(hjust = 0.5, size = 16, face = "bold"),
axis.title.x = element_text(size = 12),
axis.title.y = element_text(size = 12)
) +
annotate("text", x = 15, y = 100, label = regression_eq, color = "brown", size = 5, hjust = 0)
#3 単回帰分析 lm(目的変数~説明変数, data)
#4, 5で、散布図+単回帰直線の図が作成できます。
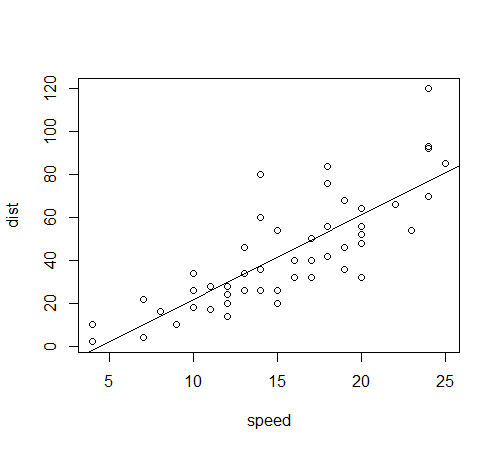
#6 β0とβ1の算出
β0=-17.579095 β1=3.932409 が求まりました。
yi=3.93xi -17.58 の式で、xiを入れると予測値yiが求まる単回帰直線の式ができました。
#7 単回帰分析の結果の詳細
Multiple R-squared(決定係数): 0.6511
Adjusted R-squared(自由度調整済み決定係数 変数の数で補正): 0.6438
これらの決定係数は、0~1の間の値をとり、モデルがどの程度yを説明できているかを示す指標になります。
p-value(p値): 1.49e-12 で、0.05以下であるため、xがyを説明する力が十分であると結論できました。
#8 intercept(切片)が正の場合は、regression_eq <- paste0(“y = “, slope, “x”, “+”, intercept) で+を入れます。
4. 単回帰の当てはまり具合を、残差分析で確認(残差プロット, Q-Qプロット)
残差分析によって、単回帰の当てはまり具合を確認します。
par(mfrow=c(1,2)) #8 plot(cars_lm, which=1:2) #9
plot関数で、残差に関するグラフは6つ指定できます。
今回は、その中の”「残差プロット」と「Q-Qプロット」を作図指定しました。
#8 複数の図を表示する指示で、1行に2つ作図の指示です。
#9 残差分析の1:残差プロットと2:Q-Qプロットを指定しています。
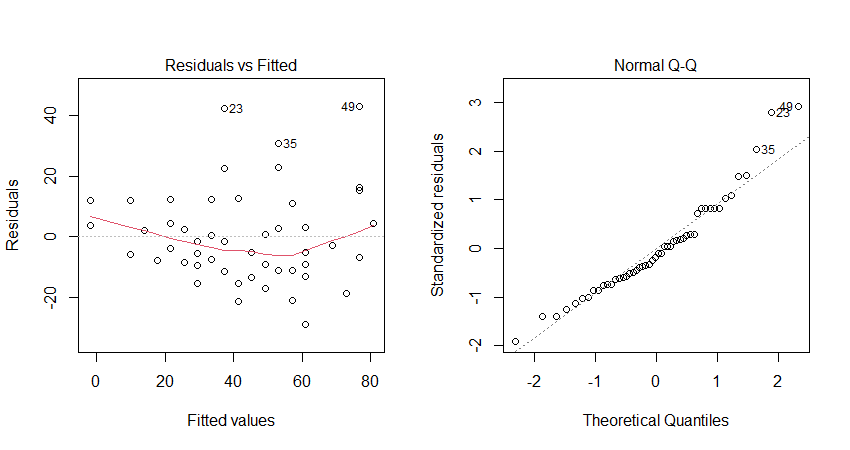
★残差プロット(上記左図)
横軸に予測値、縦軸に残差をプロットしています。
赤線は残差を説明する回帰曲線で、残差=0と重なっているほど、あてはまりがよい回帰モデルであるといえます。
図中の23, 35, 49※は、データフレームの行番号であり、このデータが、残差の絶対値が大きいものになります。
★Q-Qプロット(quantile-quantile plot 上記右図)
横軸に標準正規分布の分位点、縦軸に残差の分位点をプロットしています。
正規分布である場合、データ プロットは直線になります。
23, 35, 49※は、残差プロット同様、残差の絶対値が大きく、正規分布から外れていると考えられます。
※これらが外れ値の候補になることもあります。ただし、外れ値として取り除くかは慎重な検討が必要です。
単回帰分析の記事を、参考にしていただき、ありがとうございました。
以下のサイトにRでの重回帰分析について書いていますので、閲覧いただけると幸いです。
参考図書▼▼▼




t-120x68.png)

コメント