臨床現場で白血病患者の治療をしない群(コントロール群)と治療群の生存時間のデータを取得している。
取得データから、各群の白血病患者の生存時間を予測したい。
また、コントロール群と治療群の2群のデータがあり、それらの2群の比較も合わせて行いたい。

治療ごとに生存時間に違いがあるかを知るのに使用されるのが、生存時間解析(カプラン・マイヤー曲線、ログランク検定)です!!
生存時間解析とは、生物の死や機械システムの故障など、1つの事象(event、イベント)が発生するまでの予想される期間を分析する統計学の一分野である。
引用:Wikipedia
この生存時間解析は、臨床研究において使われます。
ある疾患をもつ患者の生存時間のデータをもとに、生存時間の予測を行うなどがあります。
臨床研究において広く使用されるt検定については、以下をご参照ください。
-160x90.png)
t-160x90.png)
また、生存時間解析は、マーケティングでも広く使用されているようです。
例えば、ある契約の解約までの期間のデータをもとに、解約期間の予測を行うなどです。


これにより、お客様により長く契約してもらえる内容であるかなどを検証することができます。
今回は、臨床研究のデータセットを用いて、生存時間解析で広く使用されるカプラン・マイヤー曲線とログランク検定についてRで作図・検定を行います。
1. カプラン・マイヤー曲線
この度使用するデータセットはgehanというMASSパッケージ内にあるものです。
gehan 白血病患者の寛解期
42人の白血病患者の試験から得られたデータフレーム。一部の患者は6-mercaptopurineで治療され(治療群)、残りはコントロール群である。この試験はマッチドペアとしてデザインされ、どちらかが寛解に至った時点で両者が試験から脱落(打ち切り)とした。
library(survival)
head(gehan) #1
# pair time cens treat
#1 1 1 1 control
#2 1 10 1 6-MP
#3 2 22 1 control
#4 2 7 1 6-MP
#5 3 3 1 control
#6 3 32 0 6-MP
Surv(gehan$time,gehan$cens) #2 打ちきりデータ+
#[1] 1 10 22 7 3 32+ 12 23 8 22 17 6 2 16 11
#[16] 34+ 8 32+ 12 25+ 2 11+ 5 20+ 4 19+ 15 6 8 17+
#[31] 23 35+ 5 6 11 13 4 9+ 1 6+ 8 10+
survfit_t <- survfit(Surv(time, cens)~treat, data=gehan,type = "kaplan-meier")#3 生存曲線データの作成
survfit_t #4
#Call: survfit(formula = Surv(time, cens) ~ treat, data = gehan)
# n events median 0.95LCL 0.95UCL
#treat=6-MP 21 9 23 16 NA
#treat=control 21 21 8 4 12
summary(survfit_t) #5 各群の概要
#Call: survfit(formula = Surv(time, cens) ~ treat, data = gehan)
# treat=6-MP
#time n.risk n.event survival std.err lower 95% CI upper 95% CI
# 6 21 3 0.857 0.0764 0.720 1.000
# 7 17 1 0.807 0.0869 0.653 0.996
# 10 15 1 0.753 0.0963 0.586 0.968
# 13 12 1 0.690 0.1068 0.510 0.935
# 16 11 1 0.627 0.1141 0.439 0.896
# 22 7 1 0.538 0.1282 0.337 0.858
# 23 6 1 0.448 0.1346 0.249 0.807
# treat=control
#time n.risk n.event survival std.err lower 95% CI upper 95% CI
# 1 21 2 0.9048 0.0641 0.78754 1.000
# 2 19 2 0.8095 0.0857 0.65785 0.996
# 3 17 1 0.7619 0.0929 0.59988 0.968
# 4 16 2 0.6667 0.1029 0.49268 0.902
# 5 14 2 0.5714 0.1080 0.39455 0.828
# 8 12 4 0.3810 0.1060 0.22085 0.657
# 11 8 2 0.2857 0.0986 0.14529 0.562
# 12 6 2 0.1905 0.0857 0.07887 0.460
# 15 4 1 0.1429 0.0764 0.05011 0.407
# 17 3 1 0.0952 0.0641 0.02549 0.356
# 22 2 1 0.0476 0.0465 0.00703 0.322
# 23 1 1 0.0000 NaN NA NA
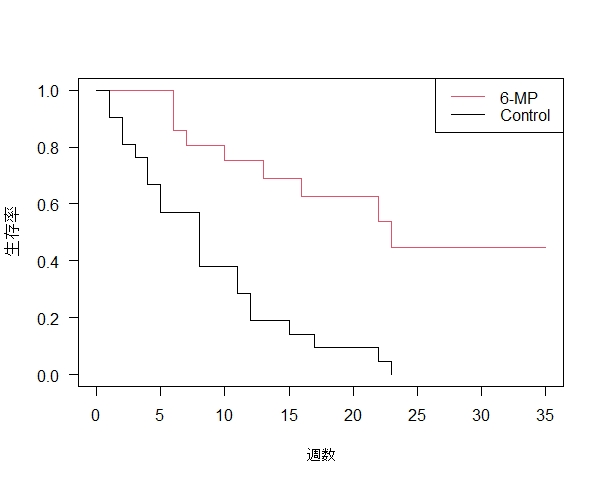
plot(survfit_t, conf.int=FALSE, las=1, xlab="週数", ylab="生存率",col=2:1) #6 カプランマイヤー曲線プロット①
legend("topright", c("6-MP", "Control"), lty=1, col=2:1) #7 凡例
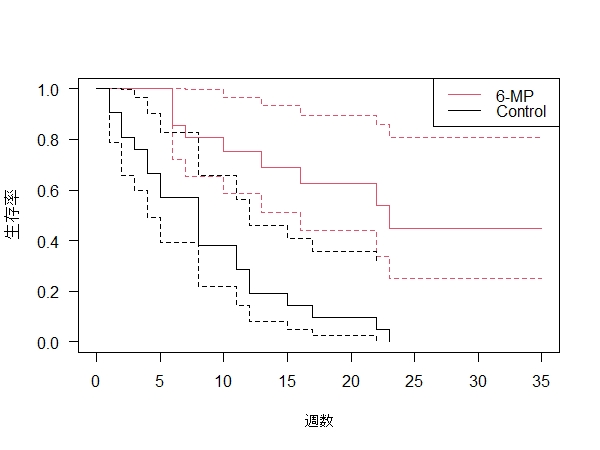
plot(survfit_t, conf.int=TRUE, xlab="週数", ylab="生存率",col=2:1) #8 カプランマイヤー曲線プロット②
legend("topright", c("6-MP", "Control"), lty=1, col=2:1)
#1 gehanデータ pair:マッチドペアの人は同じID、time:週数、cens:打ち切り(生存)0/死亡1、treat:コントロール群control/治療群(6-MP 6-mercaptopurine薬名)
#2 censで打ち切りデータには+を付けます。
+は12個でした。
#3 treatデータ別で、生存時間timeと打ち切りcensデータから生存曲線データを作成します。
#4 生存確率50%(median)treat=6-MP は 23週で、treat=controlは8週であることが分かりました。コントロール群に比べて、治療群の生存確率50%になるまでの期間が長いといえます。
#5 各群の生存時間(time)、生存患者数(n.risk)、死亡患者数(n.event)、生存確率(survival)、標準誤差(std.err)、95%信頼区間上下限値(lower 95% CI upper 95% CI)を作成しました。
#6, 7, 8 カプラン・マイヤー曲線プロット
conf.int=95%信頼区間表示なしFALSE、ありTRUE,
las=1で縦軸の数値横向き表示、
col=2:1で、色指定。赤:黒
①カプラン・マイヤー曲線
②カプラン・マイヤー(95%信頼区間上下限あり)
2群の生存分布を比較する仮説検定です。
re<-survdiff(Surv(time)~treat,data=gehan) #9 re #Call: #survdiff(formula = Surv(time) ~ treat, data = gehan) # N Observed Expected (O-E)^2/E (O-E)^2/V #treat=6-MP 21 21 29.2 2.31 8.97 #treat=control 21 21 12.8 5.27 8.97 # Chisq= 9 on 1 degrees of freedom, p= 0.003
#9 ログランク検定を実施します。p値=0.003であり、有意水準0.05とした場合、コントロール群と治療群は差があるといえることが分かりました。
以上より、治療群の方が、生存確率50%までになる期間が長く、生存分布において治療群とコントロール群は有意な差があるという結果となりました。
この手法は、臨床データのみならず、マーケティングでも広く使えるようですので、同様の解析方法でも試していただければと思います。



コメント