まなびの目標🎯
・時間と共に変化する時系列データから、時系列分析を行って将来を予測してみよう!
・2つの異なるデータの関係性(相関関係)を調べよう!
・散布図と回帰直線を使って、データ間の関係を説明しよう!
・相関関係と因果関係の重要な違いを理解しよう!
1. はじめに
2. 時系列分析
3. 2つのデータの関係を探る ~相関と回帰分析~
3.1 散布図
3.2 正の相関、負の相関、無相関
3.3 回帰分析と回帰直線
4. 【重要】相関関係と因果関係は違う!~騙されないためのデータリテラシー~
5. まとめ
6. 確認クイズ
1. はじめに
 「来月のコンビニの売上は上がるか?」
「来月のコンビニの売上は上がるか?」
「身長が高い人ほど、足のサイズも大きいというけど、本当?」
私たちの周りには、このような予測や関係性に関する疑問がたくさんあります。
データ分析の大きな目的の一つは、こうした疑問に答えること、です!
本記事では、データの中に隠されたパターンを見つけ出し、未来を予測したり、物事の関係性を調べたりするためのツール、時系列分析と回帰分析の基本的な考え方を学んでいきましょう。
2. 時系列分析
時系列データとは、時間の経過と共に記録されたデータのことです。
例:日々の気温の変化、毎月のスマートフォンの通信量、お店の売上など。
時系列分析とは、時系列データを分析し、その中に隠された意味のあるパターンや規則性を見つけ出すための手法です。過去から現在までのデータの動きを詳しく調べることで、そのデータが持つ特徴を理解し、将来の値を予測することを目指します。
使用例:ビジネスでの売上予測、株価の分析、気象予測など。
例えば、ウェブサイトの月間アクセス数の1年を通した変化を見てみます。
個人のブログサイトの、過去12ヶ月間のアクセス数(PV数)、というダミーデータを用意しました。7月にSNSで話題になり、一時的にアクセスが急増したという設定です。
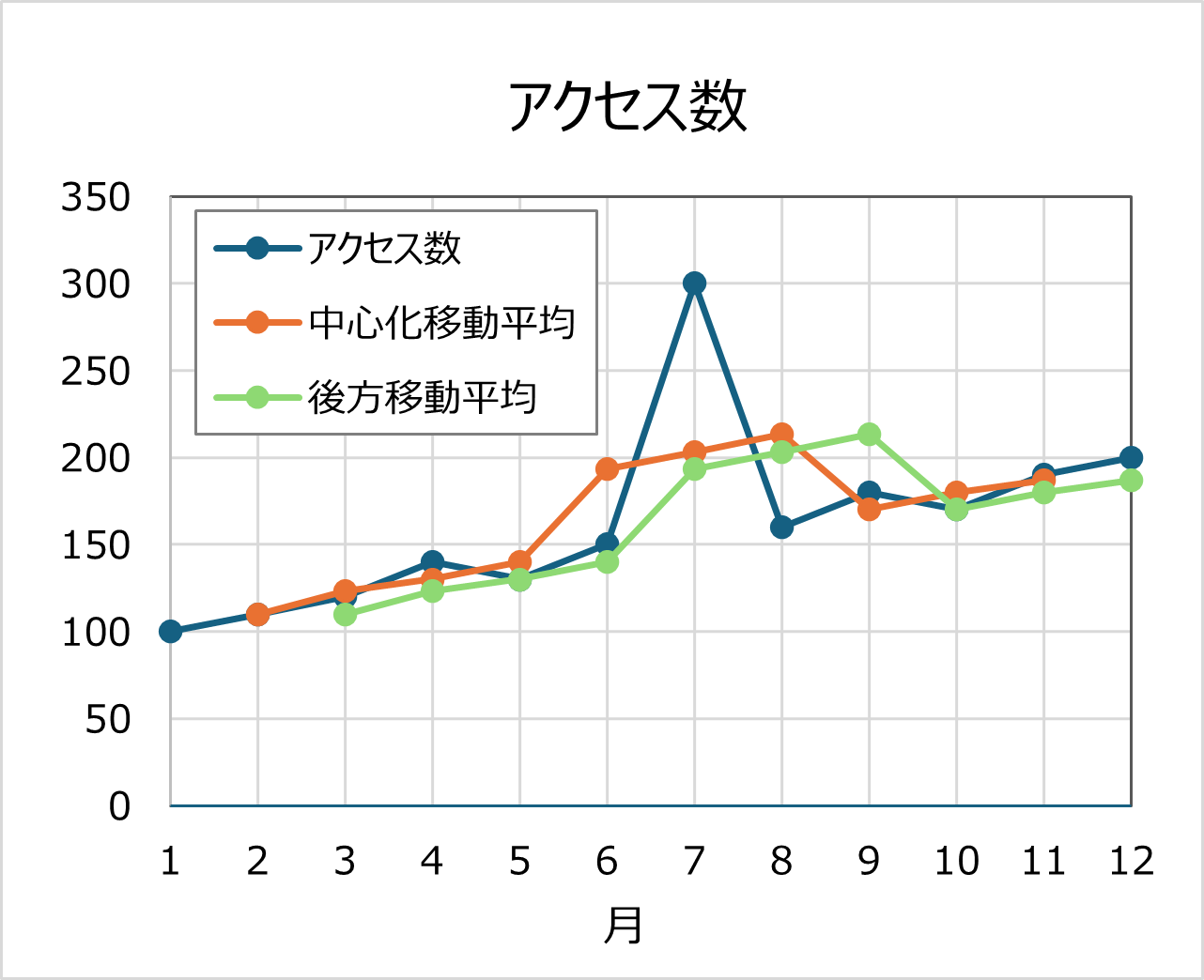
上のグラフを見ると、元のデータ(青色)に比べ、中心化移動平均(オレンジ色)と後方移動平均(黄緑色)の線は、どちらも滑らかになっているのが分かります。また、アクセス数が長期的に上昇しているという傾向も、より明確に読み取ることができます。
全体の傾向をつかむ中心化移動平均は元のデータの中心を捉えているのに対し、短期的な予測などに使われる後方移動平均は少し遅れて動きます。
目的に応じた分析手法の使い分けが重要です💡
【補足】移動中央値法
7月の突出した値(外れ値)に注目してみましょう。いずれの移動平均でも、この7月の大きな値に引っ張られて、6月〜9月にかけて大きく上に膨らんでいます。平均値の代わりに中央値を使うと、異常値に引っ張られず、より安定した傾向を見ることができます。
【発展】その他の時系列分析手法
移動平均法以外にも、時系列分析には様々な手法があります。
・季節調整: 夏に売上が増える、週末にアクセスが増えるといった、周期的な季節変動のパターンを取り除き、より本質的な変動を分析する手法です。
・自己回帰モデル (ARモデル): 「今日の値は、昨日の値に影響されている」という考え方に基づき、過去の自分自身のデータを使って未来を予測するモデルです。
3. 2つのデータの関係を探る ~相関と回帰分析~
2種類のデータに、どのような関係があるのかを知りたい!!
そんな時には、相関関係を調べ、その関係を数式で表す回帰分析を行うことがとても役立ちます。
相関とは、2種類のデータの間にある関連性の度合いのことです。「片方が増えるとき、もう片方も増える(または減る)傾向があるか」という、関係の有無や方向性を示します。
回帰分析とは、その関係性がどのくらい強いのかを調べ、数式(モデル)で表すための統計的な分析手法です。数式で表すことで、片方の値からもう片方の値を予測することも可能になります。
3.1 散布図
日中の平均気温とアイスの売上個数のように、2種類のデータの間に関係があるかどうかを調べます。
★日中の平均気温とアイスの売上個数のデータ
| 日中の平均気温 (°C) | アイスの売上個数 |
| 24 | 55 |
| 17 | 25 |
| 30 | 90 |
| 22 | 40 |
| 28 | 75 |
| 15 | 18 |
| 32 | 105 |
| 18 | 22 |
| 25 | 52 |
| 31 | 85 |
| 20 | 35 |
| 27 | 70 |
このような2つの量の関係性を調べるのに最適なグラフが散布図です。今回のデータだと、横軸と縦軸に、平均気温と売上個数をとり、対応する値にプロットしていきます。
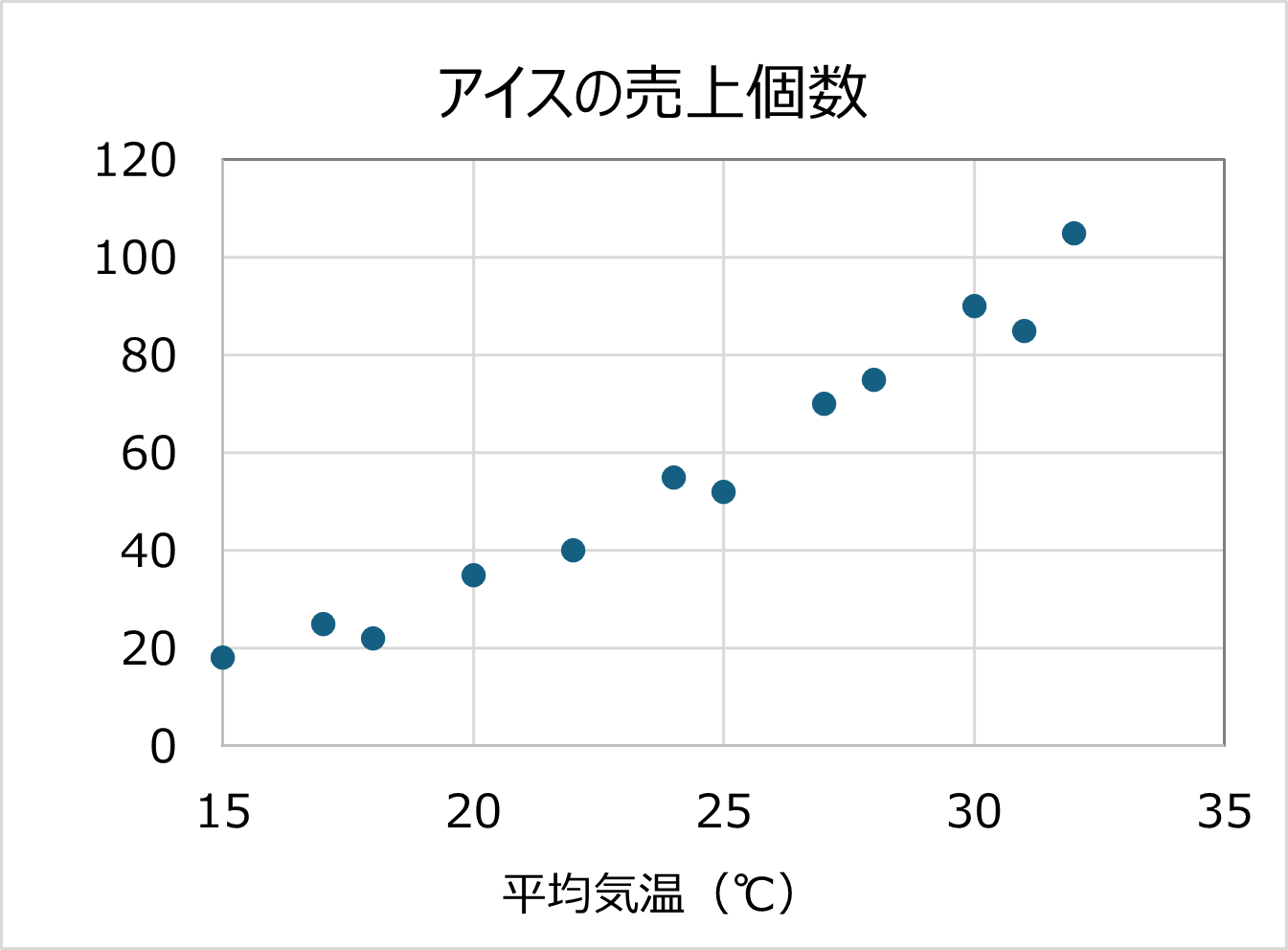
この散布図により、平均気温が上がるほど、アイスの売上個数が増加する傾向があることが分かりました。
3.2 正の相関、負の相関、無相関
散布図のプロットの分布から相関関係を読み取ることができます。相関関係には主に3つの種類があります。
正の相関: 片方のデータが増加すると、もう片方も増加する傾向。プロットが右上がりに分布する。(例:身長と体重、勉強時間とテストの点数)
負の相関: 片方のデータが増加すると、もう片方は減少する傾向。プロットが右下がりに分布する。(例:気温と暖房器具の売上)
無相関: 2つのデータに明確な関係が見られない。プロットの分布に規則性がない。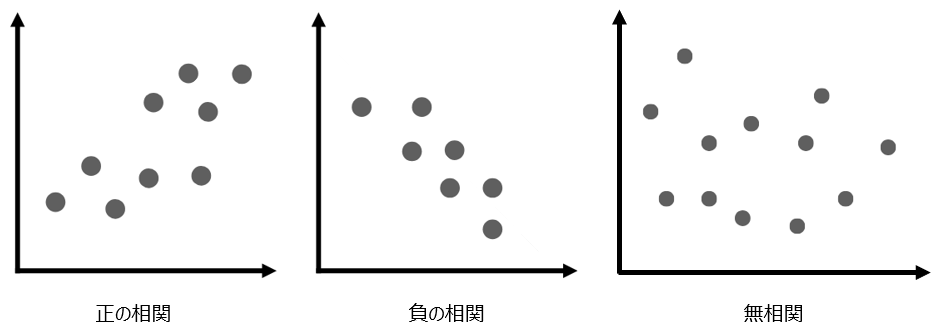
3.3 回帰分析と回帰直線
散布図でデータに正の相関や負の相関が見られたとき、「もし、このバラバラの点の真ん中を、だいたいこんなデータかな?というのを無理やり一本の直線で表すとしたら?」と考えるのが回帰分析の出発点です。
回帰分析では、2つのデータの関係性を分析し、その関係を最もよく表す一本の数式(モデル)を求めます。そして、その数式をグラフ上に描いたものが回帰直線です。
回帰直線は、散布図上のすべてのプロットから例えば平均的に最も距離が近くなるように引かれた、データ全体の傾向を要約した線です。
回帰直線によってできること💡
1. 関係性の強さを知ること
散布図の点が、回帰直線の周りに密集しているほど強い相関がある、広く散らばっているほど弱い相関があると言えます。この強さは、-1から1の値をとる「相関係数」という指標で正確に測ることができます。
※正の相関の図
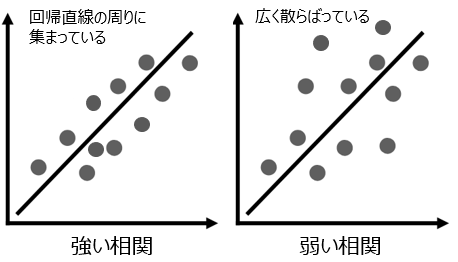
2. 未知の値を予測すること
回帰直線は、2つのデータの関係性を数式(y = ax + b のような一次関数)で表したものです。
そのため、分かっている方のデータ(x)を数式に代入することで、もう片方のデータ(y)がどうなるかを予測できます。
例:上述の★日中の平均気温(x)とアイスの売上個数(y)のデータの関係から回帰直線を求めます(Excel使用)。
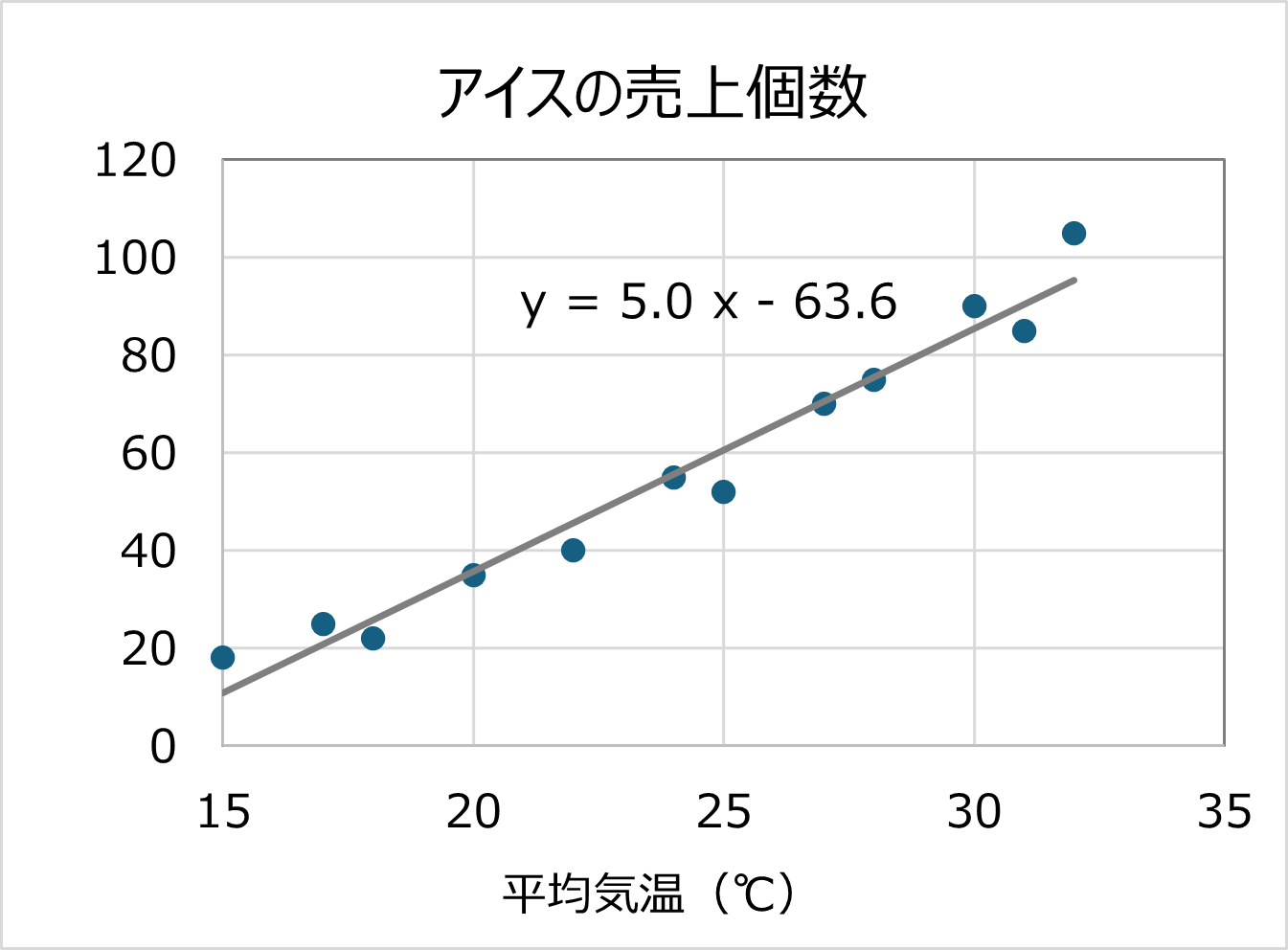 ※Excelのグラフ横の+から近似直線をチェックすると、最小二乗法で回帰式をいれることができます!
※Excelのグラフ横の+から近似直線をチェックすると、最小二乗法で回帰式をいれることができます!
明日の気温が30℃と分かっているなら
y=5.0*30-63.6 =86.4個
アイスはおそらく約86個売れるだろうといった予測ができます💡
4. 【重要】相関関係と因果関係は違う!
データ分析をする上で、重要なのは相関関係と因果関係の混同です。
例えば、ある地域のデータで「月別のアイスの売上」と「月別の熱中症の発生件数」を調べると、おそらく強い正の相関が見られるでしょう。
では、このデータを見て「アイスを食べると、熱中症になりやすくなる」と結論づけては、絶対にダメです!
これは、両方の原因となる気温が高いという、見えない要因(これを潜在因子や交絡因子と呼びます)が存在するからです。
・気温が上がる → アイスが売れる
・気温が上がる → 汗をかきやすく、熱中症になる人が増える
このように、2つのデータに相関関係があっても、それが原因と結果の関係(因果関係)であるとは限りません。「なぜこのような関係が生まれるのだろう?」と多角的に考えることはとても大切です。
5. まとめ
・時系列分析は、時系列データのパターンを読み解き、将来を予測する手法です。
・短期的な変動が大きいデータは、移動平均法などで平滑化すると、長期的な傾向が見やすくなります。
・相関とは、2つのデータが連動して動く関係性のことで、散布図で視覚的に確認できます。
・回帰分析は、データ全体の傾向を最もよく表す一本の回帰直線(数式モデル)を求め、関係性の分析や予測に利用します。
・データ間に相関関係があっても、それが「原因と結果」を意味する因果関係であるとは限りません。背景にある別の要因を考えることが大切です。
6. 確認クイズ
Q1. 時系列データのギザギザした短期的な変動をならして、長期的な傾向を見やすくするために使われる手法は何ですか?
- 移動平均法

- 因果関係

- 回帰分析

![]() 正解!
正解!
![]() 不正解!
不正解!
移動平均法
ヒント:区間を一つずつ「移動」させながら「平均」を計算していく手法でしたね。
Q2. 移動平均法のうち、過去のデータ全体の傾向をより正確に分析するのに適しており、計算結果を区間の中心にプロットする方法を何と呼びますか?
- 単純移動平均

- 中心化移動平均

- 後方移動平均

![]() 正解!
正解!
![]() 不正解!
不正解!
中心化移動平均
ヒント:プロットする位置が、区間の「中心」であることから、その名前がついています。
Q3. 2種類のデータ(例:気温とアイスの売上)の関係性を視覚的に確認するために、点をプロットして作成するグラフは何ですか?
- 散布図

- 折れ線グラフ

- 箱ひげ図

![]() 正解!
正解!
![]() 不正解!
不正解!
散布図
ヒント:2つの量の関係を見るために、点が「散らばった」ようにプロットされる図でした。
Q4. 散布図の点が全体的に右下がりの分布を示しているとき、2つのデータにはどのような関係があると言えますか?
- 無相関

- 負の相関

- 正の相関

![]() 正解!
正解!
![]() 不正解!
不正解!
負の相関
ヒント:片方が増えると、もう片方が減る、という「負(マイナス)」の関係性です。
Q5. 散布図に描かれたデータ全体の傾向を最もよく表す一本の直線を使い、片方の値からもう片方の値を予測する分析手法を何と呼びますか?
- 回帰分析

- 時系列分析

- 因子分析

![]() 正解!
正解!
![]() 不正解!
不正解!
回帰分析
ヒント:データ全体の傾向を表す「回帰直線」を求める分析手法です。
確認クイズは、いかがでしたでしょうか?今回の学習内容が、皆さんの情報活用能力を高める一助となれば幸いです。閲覧いただき、ありがとうございました!![]()
※本記事 教科書該当範囲
| 教科書名 | 該当章 |
| 新編情報Ⅰ(東京書籍) | – |
| 最新情報I(実教出版) | 第5章 2節 4. データ分析の手法 |
| 高校情報ⅠJavaScript(東京書籍) | 第5章 28. 時系列分析と回帰分析 |
| 高校情報ⅠPython(東京書籍) | 第5章 28. 時系列分析と回帰分析 |
本サイトは、教科書をベースに構成しています。使える「情報Ⅰ」を目指し、毎週月曜日に新しい記事を発信予定です。



本記事に対し、お気づきの点ございましたらお問い合わせよりご連絡頂けますと幸いです。


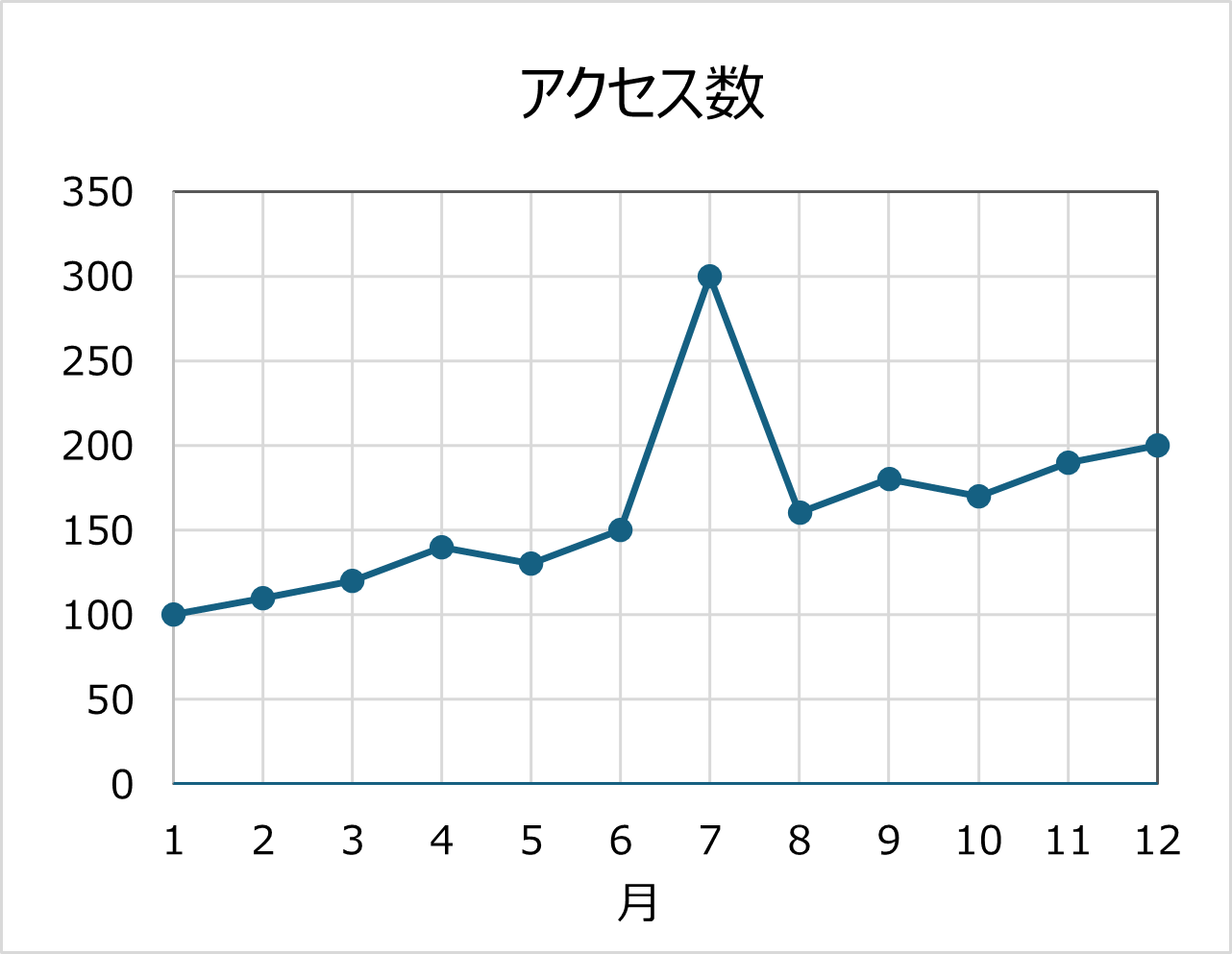 7月にアクセス数が激増、は、わかりますね。全体の傾向としては、なんとなく、増加している?ように見えなくもないです、、
7月にアクセス数が激増、は、わかりますね。全体の傾向としては、なんとなく、増加している?ように見えなくもないです、、



コメント