まなびの目標🎯
・基本統計量を知ろう!データの全体の傾向をつかむのは大事!
・データの中心や散らばりを把握することの重要性を理解しよう!
・データの分布を可視化する方法を知ろう!
最後、確認クイズもありますので、是非見ていって下さい♬
1. 基本統計量とは
2. データの中心 ~代表値(平均値・中央値・最頻値)~
3. データの散らばり ~分散と標準偏差~
4. データの分布を可視化 ~ヒストグラムと箱ひげ図~
5. まとめ
6.確認クイズ
1. 基本統計量とは

「A組とB組の数学のテスト平均点は、どちらも65点でした。」
「・・・ということは、A組もB組も、テスト範囲への理解度は同じ感じですかね!」
・・・??
平均点だけを見て、その集団を判断するのは、重要なことを見落としているかもしれません。。
平均点も、もちろん重要な情報ですが、
同じ平均点だとしても、例えば、
A組は全員が60点~70点の間に固まっている安定したクラスで、
B組は0点台と100点に近い生徒に二極化しているクラスだった場合、
2つの組が、全体の理解度が同じ感じか?といわれると、かなり違いますよね。
こういう場合は、各クラスにおける点数のばらつきや最高得点・最低得点などの情報をしることで、より具体的な判断ができるようになります!
このようにデータの傾向をつかむのに重要になるのが基本統計量です!
基本統計量とは、データ全体の分布や特徴を要約する数値のことをいいます。平均値や中央値でデータの中心を、標準偏差でばらつきを、最大値・最小値でデータの範囲などを把握するために用いられます。
この記事では、データの本質を把握するため、基本統計量と、データを視覚的に把握できるヒストグラムと箱ひげ図について説明します。
★飲料水のボトル充填ライン(ラインAとラインB)を例として、一緒に見ていきましょう!
飲料メーカーの工場に、ジュースを300mlの瓶に詰める2つの生産ライン、ラインAとラインBがあります。どの程度正しく充填されているか確認するため、各ラインから10本ずつサンプルを抜き取り、内容量を測定しました。
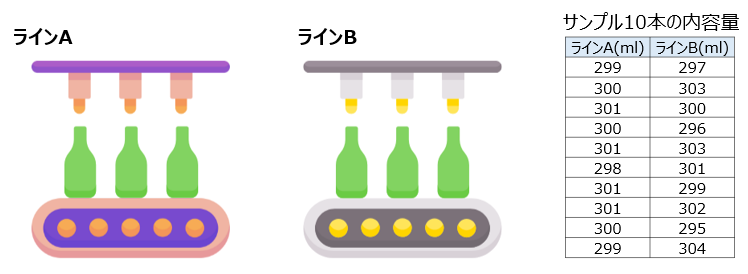
💡実際の現場でも、安定した生産の為、このような抜き取りサンプルによる品質チェックを行います!
2. データの中心 ~代表値(平均値・中央値・最頻値)~
データ全体を代表する値、代表値について学びます。
・平均値 (Mean): 最もよく使われる代表値で、全てのデータを足して、データの個数で割った値です。極端に大きい・小さい値(外れ値)があると、そちらに引っ張られてしまう性質がある点は、注意が必要です。
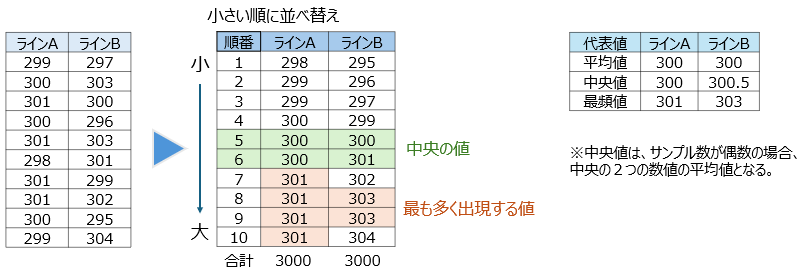
・中央値 (Median): データを小さい順に並べたときの、順番が真ん中になる値です。外れ値の影響を受けにくいです。データ数が偶数のときは、中央の2つの平均値を中央値とします。
・最頻値 (Mode): データの中で、最も頻繁に出現する値です。
★ラインAとラインB
3. データの散らばり ~分散と標準偏差~
データが代表値の周りにどれくらい散らばりがあるかを見ます。
・分散 (Variance): 各データと平均値の差を2乗し、その合計をデータ数で割った値です。散らばりが大きいほど、分散も大きくなります。
1⁄n
・σ2(シグマの2乗): 分散
・n: データの総数
・∑(シグマ): 続くカッコの中を全てのデータ(i=1 から n まで)で計算して合計
・i: i番目のデータの値
・x: 全データの平均値
・標準偏差 (Standard Deviation): 分散の平方根をとった値です。単位が元のデータと同じになるため、散らばりの度合いをより直感的に理解しやすくなります。標準偏差が大きいほど、データは広く散らばっていると言えます。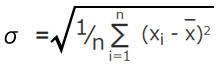
★ラインAとラインB
・ラインA(平均300)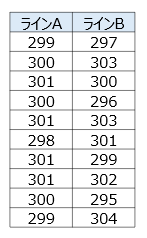
分散: σ2=1/10×((299-300)2+(300-300)2+(301-300)2+・・・) =1.111・・・
標準偏差: √σ2 =√1.111・・・ =1.054・・・
・ラインB(平均300)
分散: σ2=1/10×((297-300)2+(303-300)2+(300-300)2+・・・) =10
標準偏差: √σ2 =√10・・・ =3.162・・・
ラインAとラインBを比べると、分散・標準偏差ともにラインBの方が大きいです。ラインBの方がばらつきが大きいといえます。
4. データの分布を可視化 ~ヒストグラムと箱ひげ図~
数値だけでは分かりにくいデータの全体像を、目で見て理解するためのグラフとして、ヒストグラムや箱ひげ図などがあります。
・ヒストグラム:
データをいくつかの区間(階級)に分け、各区間に含まれるデータの個数(度数)を棒グラフで表したものです。データがどこに集中しているか(山の位置)、散らばり具合(山の裾の広がり)、外れ値の有無などを一目で把握できます。
★ラインAとラインB
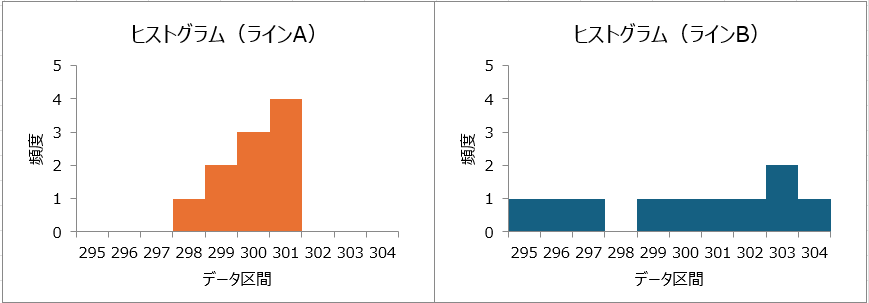
今回は、各値ごとの頻度を用いてヒストグラムを作成しました。ヒストグラムから、ラインAは中央付近にデータがまとまっており、ラインBはデータが広範囲にわたってあることが分かります。ラインBの方がデータに散らばり、ばらつきがあることがわかりました。
・箱ひげ図:
データのばらつきや分布を、箱とひげ(線)で視覚的に表現したグラフです。複数のデータグループを比較するのに利用されます。
最大値・最小値:箱ひげ図のひげの先端に書きます。ただし、外れ値を除いた最大値・最小値となることもあります。
第1四分位数:小さい方から数えて、データの1/4(25%)の位置にある値です。箱の下部の線。
第2四分位数:データの中央、1/2(50%)の位置にある値(中央値)です。箱の中央の線。
第3四分位数:小さい方から数えて、データの3/4(75%)の位置にある値です。箱の上部の線。
★ラインAとラインB
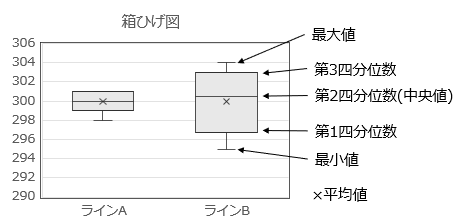
箱ひげ図より、ラインAとラインBは平均値は同じであるものの、ラインBの方が最小値と最大値の幅も広く、第1四分位数と第3四分位すうの幅も大きいことが分かりました。ラインBデータのばらつきがあることが、箱ひげ図からも分かりました。
5. まとめ
今回は、以下を中心に学びました。
・データの性質を正しく理解するには代表値(中心)と散らばりの両方を見る必要がある。
・代表値には平均値・中央値・最頻値、散らばりを見る指標には分散・標準偏差があり、これらを基本統計量とよぶ。
・データの分布はヒストグラム・箱ひげ図で可視化して確認する。
ラインAとラインBについては、平均値は同じでしたが、基本統計量やデータの可視化を確認することによって、品質の安定性において明確な違いがあることがわかりました。このように、製品の品質を一定に保つことが重要な製造業の現場では、統計的な手法が日常的に活用されています。
正確であるか(平均値が目標に近いか)、ばらつきが少ないか(標準偏差が小さいか)という2つの視点は重要で、これらも含め、常に厳しい品質チェックが行われています。
今回学んだ基本統計量やグラフを使った可視化は、まさにそのために使われる実践的な技術です。これらの手法によって品質が管理され、私たちは品質の良い製品を手に取ることができます。
6. 確認クイズ
Q1. 標準偏差の値が「大きい」ということは、データがどのような状態であることを示しますか?
- データが平均値から広く散らばっている

- データが平均値の近くに集まっている

- データの個数が多い

![]() 正解!
正解!
![]() 不正解!
不正解!
データが平均値から広く散らばっている
ヒント:標準偏差は、データの「散らばり具合」を表す指標でした。
Q2. データの値をいくつかの区間に分け、その個数を棒グラフで表すことで、全体の分布の形を確認できるグラフは何ですか?
- 折れ線グラフ

- 散布図

- ヒストグラム

![]() 正解!
正解!
![]() 不正解!
不正解!
ヒストグラム
ヒント:データの分布を山の形で視覚的に捉えるグラフです。
Q3. 箱ひげ図において、データ全体の真ん中50%が含まれる「箱」の部分は、何と何の間の範囲を示していますか?
- 最小値と最大値

- 平均値と中央値

- 第一四分位数と第三四分位数

![]() 正解!
正解!
![]() 不正解!
不正解!
第一四分位数と第三四分位数
ヒント:箱の端は、データを4つに分けたときの区切りの値(四分位数)で定義されていましたね。
Q4. 箱ひげ図で、箱やひげの長さが全体的に長い場合、そのデータはどのような特徴を持つと言えますか?
- ばらつきが大きい

- 平均値が大きい

- データ数が多い

![]() 正解!
正解!
![]() 不正解!
不正解!
ばらつきが大きい
ヒント:箱の端は、データを4つに分けたときの区切りの値(四分位数)で定義されていましたね。
Q. データの全体像を正しく知るには、「中心」を示す値と、特にもう一つ何に注目すべきですか?
- データの入力速度

- データの散らばり具合

- データの収集方法

![]() 正解!
正解!
![]() 不正解!
不正解!
データの散らばり具合
ヒント:平均点が同じでもクラスの様子が違う例がありました。その違いは何で表せるでしょう?
確認クイズは、いかがでしたでしょうか?今回の学習内容が、皆さんの情報活用能力を高める一助となれば幸いです。閲覧いただき、ありがとうございました!
※本記事 教科書該当範囲
| 教科書名 | 該当章 |
| 新編情報Ⅰ(東京書籍) | 4章 39. データ分析の流れ |
| 最新情報I(実教出版) | 第5章 2節 2. データ分析と表計算, 3. データの可視化 |
| 高校情報ⅠJavaScript(東京書籍) | 第5章 27. 統計量とデータの尺度 |
| 高校情報ⅠPython(東京書籍) | 第5章 27. 統計量とデータの尺度 |
本サイトは、教科書をベースに構成しています。使える「情報Ⅰ」を目指し、毎週月曜日に新しい記事を発信予定です。



本記事に対し、お気づきの点ございましたらお問い合わせよりご連絡頂けますと幸いです。






コメント