メタアナリシスは、論文などでの同じテーマの研究報告を複数統合する統計学的手法です。
複数の研究での議論を行うため、エビデンスレベルも高いとされており、医学研究において重要な役割を担っており、多くのメタアナリシスの研究論文が報告されています。
先日、メタアナリシスに関する記事を投稿しております。
以前紹介しましたメタアナリシスの流れは、以下の通りです。
①文献の収集: 対象となる研究や試験の文献収集。対象サイト（PubMed, MEDLINE, Google Scholarなど）や検索式、検索日、対象期間などは、研究の再現性の観点から記載は重要です。
②文献の選択: 収集された文献について、適格基準（研究デザイン、対象者、アウトカムなど）と除外基準に沿って選定を行う。
③データの抽出: 選定された文献からデータを抽出し、同一形式でまとめる。
④データの統合: 効果モデル（固定効果モデル or ランダム効果モデル）を用いて効果量（効果サイズ, エフェクトサイズ）の統合を行う。
⑤異質性の評価: 研究間の異質性を評価(Q統計量、I^2統計量など)し、結果の一貫性を確認する。
⑥出版バイアスの評価:ファンネルプロット、Eggerテスト、Beggテストなどで出版バイアスを検出。
⑦メタ回帰やサブグループ分析: 必要に応じて、異なる要因や条件に基づいて結果を詳細に分析する。
①～③はデータセットを利用して、前回の記事で④データの統合、⑤異質性の評価を解説しました。
本記事では、「⑥出版バイアスの評価」を解説したいと思います。
1. 出版バイアスとは
統計学的に有意な結果が得られたもの（薬剤の効果が確認された、など）は、研究論文として報告されやすい傾向があり、有意な結果を示さないものは、報告されない傾向があるといわれています（※１）。
メタアナリシスには発表された研究のみが含まれるので、実際の効果を過大に評価する可能性があります。
このことを出版バイアスと言います。
本記事では、ファンネルプロット、Egger’sテスト、Begg’sテストを用いて出版バイアスの影響を評価します。
※１ Dickersin K, Min YI. Publication bias: the problem that won’t go away. Ann N Y Acad Sci. 1993 Dec 31;703:135-46; discussion 146-8. doi: 10.1111/j.1749-6632.1993.tb26343.x.
2. ファンネルプロットで出版バイアスを視覚的に確認
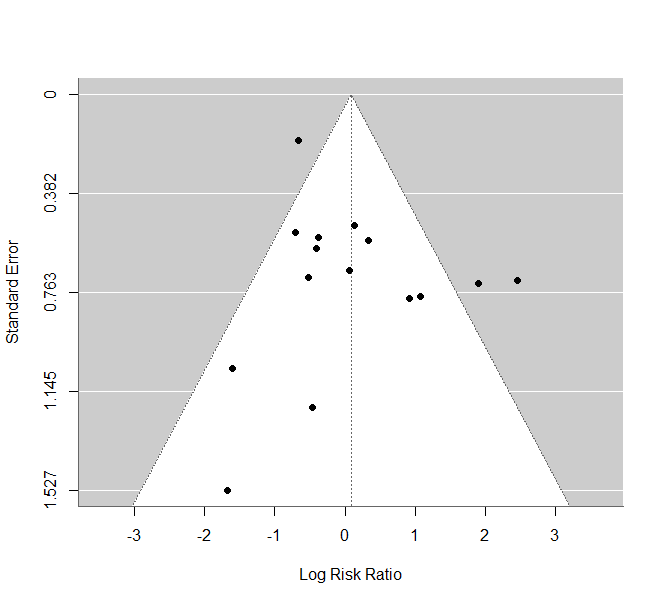
メタアナリシスの出版バイアスや小規模研究効果の影響を視覚的に評価するために用いられるのが、ファンネルプロットです。
効果サイズの精度（標準誤差）を横軸に、効果サイズ自体を縦軸にプロットし、例えば、左側に小さな研究や負の効果が偏ると、出版バイアスが示唆されます。
視覚的に歪みを検出し、結果の信頼性を評価するのに役立ちます。
前回投稿の続き、として、dat.laopaiboon2015（下気道感染症に対するアジスロマイシンの有効性に関する研究(15の研究結果のデータ)）を使用していきます。
薬剤の有効性について、研究を統合して、効果量としてリスク比（RR）を求めました。
異質性(I^2)を確認後（前回投稿参照）、ランダム効果モデルを選択し、手法としてはREML法を用いて効果量を計算しました。
この結果について出版バイアスを視覚的に確認するため、ファンネルプロットを作成します。
install.packages("metafor")
library(metafor)
head(dat.laopaiboon2015)
# author year ai n1i ci n2i age diag.ab diag.cb diag.pn ctrl
#1 Balmes 1991 4 48 7 56 adults 1 0 0 amoxyclav
#2 Beghi 1995 22 69 2 73 adults 0 1 0 amoxyclav
#3 Biebuyck 1996 53 497 53 257 adults 1 1 0 amoxyclav
#4 Daniel 1991 5 121 10 120 adults 1 0 0 amoxycillin
#5 Ferwerda 2001 5 55 7 53 children 0 0 1 amoxyclav
#6 Gris 1996 6 34 2 33 adults 1 1 1 amoxyclav
dat <- dat.laopaiboon2015
res<-rma(measure="RR", ai=ai, n1i=n1i, ci=ci, n2i=n2i, data=dat, method="REML")# RRのランダム効果モデル（REML法）
#Random-Effects Model (k = 15; tau^2 estimator: REML)
#tau^2 (estimated amount of total heterogeneity): 0.5874 (SE = 0.3897)
#tau (square root of estimated tau^2 value): 0.7664
#I^2 (total heterogeneity / total variability): 64.85%
#H^2 (total variability / sampling variability): 2.84
#Test for Heterogeneity:
#Q(df = 14) = 38.4438, p-val = 0.0004
#Model Results:
#estimate se zval pval ci.lb ci.ub
# 0.0852 0.2673 0.3186 0.7501 -0.4388 0.6092
#---
#Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
funnel(res) #ファンネルプロットデータ項目内訳（関わるもののみ抜粋）
author 著者名
year 発表年
ai アジスロマイシンを投与した群における臨床的失敗例数
n1i アジスロマイシン投与群における患者数
ci アモキシシリンまたはアモキシクラブを投与した群における臨床失敗例数
n2i アモキシシリンまたはアモキシクラブを投与した群における患者数
#ファンネルプロット
ファンネルプロットは、効果量を横軸、精度（標準誤差など）を縦軸にプロットされています。
研究数が多く、左右対称な形状であれば出版バイアスがない、または小さいと判断されます。
一方、非対称の場合は、小規模研究や否定的な結果の研究が不足している可能性があり、出版バイアスが示唆されます。
視覚的には、非対称であるように見えますが、この判断を補足する検定があり、Egger’sテストとBegg’sテストです。
3. Egger’sテストとBegg’sテストで出版バイアスを統計的に評価
3.1 Egger’sテスト（Egger検定）
Egger’sテストは、ファンネルプロットの非対称性を統計的に検出する方法で、回帰分析に基づいています。
帰無仮説：ファンネルプロットは対称である。（出版バイアス等による非対称性は存在しない）
対立仮説：ファンネルプロットは非対象である。（出版バイアス等が存在する可能性がある）
なお、Egger’sテストは、精度などの観点から研究数10以上を推奨されています（※２）。
※２ Recommendations for examining and interpreting funnel plot asymmetry in meta-analyses of randomised controlled trials doi:10.1136/bmj.d4002
regtest(res, model = "lm") #Regression Test for Funnel Plot Asymmetry #Model: weighted regression with multiplicative dispersion #Predictor: standard error #Test for Funnel Plot Asymmetry: t = 1.8088, df = 13, p = 0.0937 #Limit Estimate (as sei -> 0): b = -0.7992 (CI: -1.5715, -0.0270)
p値0.0937であり、有意水準0.05とした場合、統計学的に有意であるとは言えず、帰無仮説を棄却することはできませんでした。出版バイアスがあるとは言い切れない結果でした。
b値(標準誤差（SE）が0に近づいた場合の効果量（バイアスの推定値）)-0.7992で負あり、ファンネルプロットの左側にデータ多く、b値の信頼区間(CI: -1.5715, -0.0270)に0が含まれておらず、効果量の非対称性がある可能性が示唆されます。
p値とb値での判断が異なることは、研究数の少なさや、異質性の高さなど、原因が考えられます。
こういった場合も含め、Egger’sテスト単独ではなく、Begg’sテストやファンネルプロットも含む包括的な判断を行います。
3.2 Begg’sテスト（Begg検定）
Begg’sテスト（Begg and Mazumdar’s Rank Correlation Test）は、効果量と標準誤差についてKendallの順位相関係数に基づき、ファンネルプロットの非対称性を検出します。
ranktest(res) #Rank Correlation Test for Funnel Plot Asymmetry #Kendall's tau = 0.0857, p = 0.6972
ファンネルプロットが対称であり、出版バイアスの可能性が低いといえます。
4. まとめ
ファンネルプロットで左側にプロットが多く偏っていて、出版バイアスの存在が考えられます。
しかし、Egger’sテスト(p=0.0937）やBegg’sテストの結果（p = 0.6972）は統計的に有意ではなく、出版バイアスの証拠としては明確ではありませんでした。
プロットの視覚的な非対称性と統計検定の結果を総合的に考慮すると、出版バイアスの可能性を否定しきれないため、慎重な解釈が求められます。
異質性や他の要因も非対称性に影響を与える可能性があるため、これらを考慮した追加の解析（メタ回帰やサブグループ解析）を行うなどで、さらに解釈を進めていくことができます。
後日、メタ回帰やサブグループ解析についても記事をアップしたいと思います。
その他参考文献
Lee YH. An overview of meta-analysis for clinicians. Korean J Intern Med. 2018 Mar;33(2):277-283. doi: 10.3904/kjim.2016.195.
コメント