Rでロジスティック回帰分析　ー二値の予測・分類、ステップワイズ法、ROC曲線－

今回は、Rでのロジスティック回帰分析について解説します。
ロジスティック回帰は、目的変数が0か１かの予測・分類するのに役立つ統計手法です。

例えば、ある事象が「起こる」か「起こらない」かの”二値”の目的変数を説明変数を用いて予測する、など。
💡 この商品を購入率は？購入するか、しないかを予測！この予測にはどんな理由が影響を与えるか？　（マーケティング分野）
💡 病気を患った場合の2年後の生存率は？どんな因子が影響を与えるか？　（医療分野）　など

■目次
1.　ロジスティック回帰分析とは
2.　Rでロジスティック回帰モデルの実装（変数選択：ステップワイズ法, AIC）
3.　モデルの精度評価：ROC曲線による分析
4.　まとめ

1. ロジスティック回帰分析とは

ロジスティック回帰分析は、二値の結果（例：生存/死亡、購入/非購入）を予測するための統計手法です。
予測したい目的変数の二値（0/1）に対し、どの説明変数（年齢、収入など）がどのように影響を与えるかなどを算出することができます。
医療、マーケティングなど幅広い分野で利用されています。

今回は、医療分野でのロジスティック回帰分析についてRのコード例も含めて解説していきたいと思います。

以前、生存時間解析において解説しましたカプラン・マイヤー曲線やコックス比例ハザードモデルでは、生存時間の長さを考慮して予測モデルを作成しましたが、ロジスティック回帰においては生存時間の長さ自体は考慮されず、予測モデルを作成します。
例えば、ある時点での「生存/死亡」、あるいは治療効果「無/有」などの二値データを目的変数として使用し、これに影響を与える可能性のある説明変数を用いて予測モデルを作成します。

生存確率を予測する場合の注意💡
➢カプラン・マイヤー曲線&コックス回帰モデル　⇒生存時間の長さが考慮される
➢ロジスティック回帰　⇒生存時間の長さは考慮されない（ある時点の生存/死亡:0/1を目的変数とする）

Rで生存時間解析①単変数で予測　ーカプラン・マイヤー曲線,survfit関数、ログランク検定,survdiff関数ー

臨床現場で白血病患者の治療をしない群（コントロール群）と治療群の生存時間のデータを取得している。取得データから、各群の白血病患者の生存時間を予測したい。また、コントロール群と治療群の2群のデータがあり、それらの2群の比較も合わせて行...

Rで生存時間解析②複数因子でも予測できる　ーコックス比例ハザードモデル, coxph関数ー

今回は、生存時間解析として広く使用されるコックス比例ハザードモデルについて解説します。以前、生存時間解析として、カプラン・マイヤー曲線やログランク検定などの手法を紹介しました。 ■目次 1. コックス比例ハザードモデルとは（...

2. Rでロジスティック回帰モデルの実装（変数選択：ステップワイズ法, AIC）

今回は、survival パッケージに入っているpbc（原発性胆汁性胆管炎患者）のデータセットを使用します。
このデータは、1974年から1984年にかけて実施されたPBCに関する無作為プラセボ対照試験のものです。患者の年齢や、検査結果、その後の生存日数などの記録です。
age：年,albumin：血清アルブミン（g/dl）,alk.phos：アルカリホスホターゼ（U/リットル）,ascites：腹水の有無,ast：アスパラギン酸アミノトランスフェラーゼ（U/ml）,bili：血清ビリルンビン（mg/dl）,chol：血清コレステロール（mg/dl）, copper：尿中銅（ug/日）, edema：0 浮腫なし、0.5 未治療または,1 治療成功,利尿療法にもかかわらず浮腫がある, hepatato：肝腫大または肝腫大の有無,id：症例番号, platelet：血小板数,protime：標準化血液凝固時間,sex：男女,spider：皮膚の血管奇形,stage：組織学的病期（生検が必要）,status：エンドポイントでの状態、0/1/2で打ち切り、移植、死亡,time：登録から死亡までの日数、1986年7月における登録から死亡、移植、試験解析のいずれか早い時点までの日数,trt： D-ペニシラミンは1/2/NA、プラセボは無作為化せず,trg：トリグリセリド（mg/dl）

今回は、pbc患者が2年後に生存していたかどうかを予測するモデルを構築します。

◆データの前処理
➢　statusの移植データは削除　statusの１以外の打ち切り0と死亡2のサンプルのみで解析
➢　2年後の生存したかについて、time>=730（730日以上）生存/死亡を0/1とした。
このpbcデータの項目のうち、上記の青字を説明変数として用いて、変数選択も含めて予測モデルを実装していきます。（解説用に抜粋）

◆ロジスティック回帰分析手順
①2年後の生存/死亡：0/1を目的変数とし、青字の説明変数で予測モデルを作成する。
②予測モデルの変数選択にはステップワイズ法を用いる。AICの数値が一番小さい組み合わせを最適モデルとする。
③最適予測モデルの精度を確認する。

#パッケージ読み込み（インストールしていない場合は、install.packages("")）
library(survival)
library(dplyr)
library(ggplot2)

#欠損サンプル削除
pbc_n <- na.omit(pbc)

#2年後の生存/死亡：0/1にする　
pbc_n1<- pbc_n%>%
  mutate(survival_2yr = ifelse(time >= 730, 0, 1))

# フルモデル（すべての変数を含めたモデル）　①
full_model <- glm(survival_2yr ~ trt+age + albumin + alk.phos + ascites + ast + bili + chol + copper + edema + hepato + platelet + protime + sex, 
                  data = pbc_n1, 
                  family = binomial)

# 変数選択（ステップワイズ法を使用）
stepwise_model <- step(full_model, direction = "both")
#Start:  AIC=127.66
#survival_2yr ~ trt + age + albumin + alk.phos + ascites + ast + 
#    bili + chol + copper + edema + hepato + platelet + protime + 
#    sex
#           Df Deviance    AIC
#- sex       1   97.675 125.67
#- platelet  1   97.678 125.68
#- age       1   97.728 125.73
#- bili      1   97.777 125.78
#- trt       1   97.780 125.78
#- hepato    1   98.020 126.02
#- alk.phos  1   98.093 126.09
#- chol      1   98.985 126.98
#- albumin   1   99.516 127.52
#- ascites   1   99.577 127.58
#- ast       1   99.604 127.60
#<none>          97.661 127.66
#- edema     1  101.195 129.19
#- copper    1  101.260 129.26
#- protime   1  109.381 137.38

#Step:  AIC=125.68
#survival_2yr ~ trt + age + albumin + alk.phos + ascites + ast + 
#    bili + chol + copper + edema + hepato + platelet + protime
#           Df Deviance    AIC
#- platelet  1   97.692 123.69
#- age       1   97.782 123.78
#- trt       1   97.798 123.80
#- bili      1   97.807 123.81
#- hepato    1   98.041 124.04
#- alk.phos  1   98.114 124.11
#- chol      1   98.990 124.99
#- albumin   1   99.528 125.53
#- ascites   1   99.581 125.58
#- ast       1   99.625 125.62
#<none>          97.675 125.67
#- edema     1  101.205 127.20
#+ sex       1   97.661 127.66
#- copper    1  101.871 127.87
#- protime   1  109.392 135.39
・・・省略・・・
#Step:  AIC=114.87
#survival_2yr ~ albumin + ascites + ast + chol + copper + edema + 
#    protime
#           Df Deviance    AIC
#<none>          98.873 114.87
#- albumin   1  101.109 115.11
#- ascites   1  101.154 115.15
#- ast       1  101.177 115.18
#+ alk.phos  1   98.306 116.31
#- edema     1  102.378 116.38
#+ hepato    1   98.586 116.59
#- chol      1  102.594 116.59
#+ trt       1   98.739 116.74
#+ sex       1   98.771 116.77
#+ age       1   98.776 116.78
#+ platelet  1   98.778 116.78
#+ bili      1   98.851 116.85
#- copper    1  103.049 117.05
#- protime   1  112.544 126.54

# モデルの概要を確認
summary(stepwise_model)
#Call:
#glm(formula = survival_2yr ~ albumin + ascites + ast + chol + 
#    copper + edema + protime, family = binomial, data = pbc_n1)
#Coefficients:
#             Estimate Std. Error z value Pr(>|z|)    
#(Intercept) -9.118475   3.607735  -2.527 0.011488 *  
#albumin     -1.102427   0.729266  -1.512 0.130611    
#ascites      1.280659   0.859753   1.490 0.136338    
#ast          0.008883   0.005739   1.548 0.121637    
#chol        -0.002909   0.001644  -1.770 0.076783 .  
#copper       0.005973   0.002831   2.110 0.034869 *  
#edema        1.675501   0.871307   1.923 0.054483 .  
#protime      0.822629   0.221803   3.709 0.000208 ***
#---
#Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
#
#(Dispersion parameter for binomial family taken to be 1)
#    Null deviance: 189.766  on 275  degrees of freedom
#Residual deviance:  98.873  on 268  degrees of freedom
#AIC: 114.87
#Number of Fisher Scoring iterations: 6

最適なロジスティック回帰モデルは、以下の式で表されました：

logit(生存確率)=−9.118+(−1.102×albumin)+(1.280×ascites)+(0.00888×ast)+(−0.0029×chol)+(0.00597×copper)+(1.675×edema)+(0.822×protime)
この結果に基づいて、各説明変数の影響を詳しく見ていきます。

各説明変数について、Estimate（推定値）は変数が1単位増加した際の対数オッズへの影響を示します。
Pr(>|z|) の値が小さいほど、その変数の影響が大きい可能性があることを意味します。

各変数については、有意水準を0.05とした場合、copper（尿中銅濃度）とprotime（血液凝固時間）が有意な変数であり、2年後の生存/死亡に影響を与えている可能性が示唆されました。

Null devianceは、説明変数を含まないモデルの適合度を示し、値が高いほど適合度が低くなります。Residual devianceは、説明変数を含む現在のモデルの適合度を示し、値が低いほどモデルがデータに適合していることを意味します。今回の結果では、Null deviance189.766に対しResidual devianceが98.873と大幅に低下しており、モデルの適合性が改善されています。

モデルの最適化は、6回の反復（Fisher Scoring iterations） で収束しています。一般的に10回以内で収束すれば適切な収束と考えられているため、モデルの安定性も確認されました。

3.　モデルの精度評価：ROC曲線による分析

ROC（Receiver Operating Characteristic）曲線とは、一般的には予測・分類モデルの性能を評価するための手法です。今回は、生存か死亡かの二値の予測を評価します。

特異度（1-Specificity, 偽陽性率）と感度（Sensitivity, 真陽性率）の関係を視覚的に示し、モデルがどの程度うまく二値判定できるかを判断できます。

ROC曲線の下の面積（AUC）が1に近いほど、モデルの識別性能が高いことを示します。

ROC曲線による評価

#予測確率の計算
pred_probs <- predict(stepwise_model, type = "response")

#ROC曲線の作成
roc_curve <- roc(pbc_n1$survival_2yr, pred_probs)

#ROC曲線のプロット
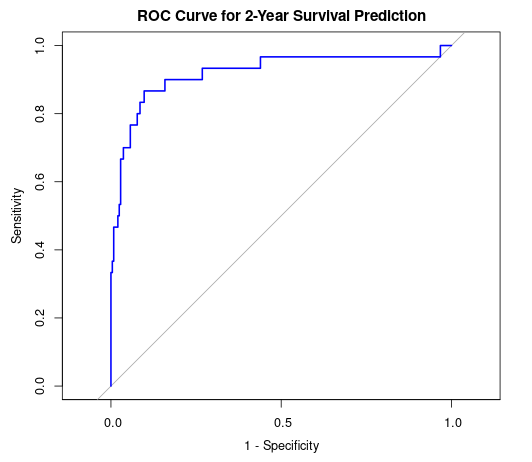
plot(roc_curve,
 col = "blue",
 lwd = 2,
 main = "ROC Curve for 2-Year Survival Prediction",
 legacy.axes = TRUE)

#AUC（Area Under the Curve）の算出
auc(roc_curve)
#Area under the curve: 0.919

ROC曲線の下の面積（AUC）の基準　参考(※１)

AUC values	Test quality
0.9-1.0	Excellent（優れている）
0.8–0.9	Very good（とてもよい）
0.7–0.8	Good（よい）
0.6–0.7	Satisfactory（満足できる）
0.5–0.6	Unsatisfactory（満足できない）

今回のモデルはAUCが0.919なので、優れているモデルであることが分かりました。

※１　Trifonova OP, Lokhov PG, Archakov AI. [Metabolic profiling of human blood]. Biomed Khim. 2014 May-Jun;60(3):281-94. Russian. doi: 10.18097/pbmc20146003281. PMID: 25019391.