前回の記事では、アンケートなどの質問項目の背後にある性格特性(潜在因子)を明らかにするための方法として、因子分析(Factor Analysis)をRで実行する手順を、コード付きで紹介しました。

因子分析は、複数の観測変数を少数の潜在因子で説明する強力な手法であり、心理的構造をシンプルに捉えるのに役立ちます。しかし、因子同士の関係性や測定誤差を明示的にモデル化できないという制限もあります。
そこで今回紹介するのが、より柔軟かつ包括的に心理データの構造を捉える手法、共分散構造分析(Covariance Structure Analysis)、別名:構造方程式モデリング(Structural Equation Modeling: SEM)です。
SEMは、因子分析の拡張として、因子間の因果的関係や誤差項も含めてモデル化・検証できるフレームワークで、心理学・教育・社会科学などの分野で幅広く利用されています。
1. 共分散構造分析とは?
共分散構造分析(SEM)は、複数の観測変数と潜在変数(因子)を同時に扱いながら、変数間の構造的な関係(因果構造)を明らかにする統計手法です。
・測定モデル(Measurement model):各潜在因子が、どの観測変数に影響するか(因子分析に相当)
・構造モデル(Structural model):潜在変数間の因果的な関係をモデル化(パス解析に相当)
モデルの良さを示す適合度指標(RMSEA, CFIなど)を通じて、統計的にモデルの妥当性を検証できます。
| 項目 | 因子分析(EFA) | 共分散構造分析(SEM) |
|---|---|---|
| アプローチ | 探索的(モデル仮定なし) | 確認的(理論に基づいてモデル指定) |
| モデル内容 | 測定モデル(観測→潜在) | 測定モデル+構造モデル |
| 変数間の因果関係 | 扱わない | 潜在変数間の因果関係も扱う |
| 可視化 | なし(数値の可視化など) | パス図によって視覚的に表現可能 |
2. 使用パッケージとデータ
library(lavaan) ?HolzingerSwineford1939 #データセットの内容確認
HolzingerSwineford1939データセット:
2つの学校の児童301人についての知能検査の得点を含む15変数からなるデータセットです。
id: 識別子
sex: 性別
ageyr: 年齢(年)
agemo: 年齢(月)
school: 学校(PasteurまたはGrant-White)
grade: 学年
x1: 視覚認知
x2: 立体の構成
x3: ひし形の認識
x4: 段落理解
x5: 文章補完
x6: 単語の意味
x7: 加算スピード
x8: 速算ドット計数
x9: 文字識別
3. モデルの定義
共分散構造分析モデルについて仮説を立てます。アンケートの背景から、visual(視覚)、textual(言語)、speed(処理速度)を潜在因子と仮定し、アンケート項目(x1~9)について、visual(視覚)はx1, x2, x3 、textual(言語)はx4, x5, x6 、speed(処理速度)はx7, x8, x9に影響を与えるものと仮定します。
※今回は、アンケート情報から潜在因子を仮定して進めますが、因子分析を用いて、潜在因子の抽出から行うこともできます!
model <- 'visual =~ x1 + x2 + x3 textual =~ x4 + x5 + x6 speed =~ x7 + x8 + x9'
上記の3つの潜在因子と、各因子を支えるアンケート項目をモデル構造として設定し、共分散構造分析を進めていきます。
4. SEM実行と適合度の評価
fit <- sem(model, data = HolzingerSwineford1939)
summary(fit, fit.measures = TRUE, standardized = TRUE)
# 出力結果
#lavaan 0.6-19 ended normally after 35 iterations
## 適合指標
# Estimator ML
# Optimization method NLMINB
# Number of model parameters 21
# Number of observations 301
#Model Test User Model:
# Test statistic 85.306
# Degrees of freedom 24
# P-value (Chi-square) 0.000
#Model Test Baseline Model:
# Test statistic 918.852
# Degrees of freedom 36
# P-value 0.000
#User Model versus Baseline Model:
# Comparative Fit Index (CFI) 0.931
# Tucker-Lewis Index (TLI) 0.896
#Loglikelihood and Information Criteria:
# Loglikelihood user model (H0) -3737.745
# Loglikelihood unrestricted model (H1) -3695.092
# Akaike (AIC) 7517.490
# Bayesian (BIC) 7595.339
# Sample-size adjusted Bayesian (SABIC) 7528.739
#Root Mean Square Error of Approximation:
# RMSEA 0.092
# 90 Percent confidence interval - lower 0.071
# 90 Percent confidence interval - upper 0.114
# P-value H_0: RMSEA <= 0.050 0.001
# P-value H_0: RMSEA >= 0.080 0.840
#Standardized Root Mean Square Residual:
# SRMR 0.065
#Parameter Estimates:
# Standard errors Standard
# Information Expected
# Information saturated (h1) model Structured
#Latent Variables:
# Estimate Std.Err z-value P(>|z|) Std.lv Std.all ## 標準化因子負荷量
# visual =~
# x1 1.000 0.900 0.772
# x2 0.554 0.100 5.554 0.000 0.498 0.424
# x3 0.729 0.109 6.685 0.000 0.656 0.581
# textual =~
# x4 1.000 0.990 0.852
# x5 1.113 0.065 17.014 0.000 1.102 0.855
# x6 0.926 0.055 16.703 0.000 0.917 0.838
# speed =~
# x7 1.000 0.619 0.570
# x8 1.180 0.165 7.152 0.000 0.731 0.723
# x9 1.082 0.151 7.155 0.000 0.670 0.665
#Covariances:
# Estimate Std.Err z-value P(>|z|) Std.lv Std.all ##潜在因子の相関
# visual ~~
# textual 0.408 0.074 5.552 0.000 0.459 0.459
# speed 0.262 0.056 4.660 0.000 0.471 0.471
# textual ~~
# speed 0.173 0.049 3.518 0.000 0.283 0.283
#Variances:
# Estimate Std.Err z-value P(>|z|) Std.lv Std.all
# .x1 0.549 0.114 4.833 0.000 0.549 0.404
# .x2 1.134 0.102 11.146 0.000 1.134 0.821
# .x3 0.844 0.091 9.317 0.000 0.844 0.662
# .x4 0.371 0.048 7.779 0.000 0.371 0.275
# .x5 0.446 0.058 7.642 0.000 0.446 0.269
# .x6 0.356 0.043 8.277 0.000 0.356 0.298
# .x7 0.799 0.081 9.823 0.000 0.799 0.676
# .x8 0.488 0.074 6.573 0.000 0.488 0.477
# .x9 0.566 0.071 8.003 0.000 0.566 0.558
# visual 0.809 0.145 5.564 0.000 1.000 1.000
# textual 0.979 0.112 8.737 0.000 1.000 1.000
# speed 0.384 0.086 4.451 0.000 1.000 1.000
◆適合度
SEMのモデル適合度として確認される指標です。複数の指標で、モデルの適合度を判断していきます。
・Chi-square(カイ二乗検定):モデルがデータと完全に一致するかを帰無仮説として検定
p value=0.000 であり、統計学的に有意であり、帰無仮説は棄却。モデルは完全には当てはまらない可能性が示唆される※。
※カイ二乗検定はサンプルサイズに敏感であり、大規模データでは些細なずれでも有意になる傾向があります。厳しい検定のため、参考程度にとどめることもあります。複数の指標を組み合わせて総合的に判断します。
・Comparative Fit Index(CFI):変数間に相関がないとしたモデルとの相対的な適合度
CFIは0.9以上が当てはまりが良いとする基準と0.95以上を良いとする基準があり、CFI=0.931は両基準周辺の数値である。
・Tucker-Lewis Index (TLI) :モデルの複雑さを加味した適合度
TLIもCFI同様の基準であるが、TLI=0.896の結果は、当てはまりが良いとは言えない結果であった。
・Root Mean Square Error of Approximation(RMSEA):誤差の大きさ
RMSEAは0.06以下を当てはまりがよいとする基準、あるいは、0.1までならmoderate fitとするという基準もある。RMSEA=0.092は、やや高めであるが、後者の基準であればmoderate fitである。
・Standardized Root Mean Square Residual(SRMR):標準化残差の平均的なずれ
SRMRは0.08以下を当てはまりが良いとする基準の提案があり、SRMR=0.065は当てはまりが良いといえる。
CFI・SRMRは良好ですが、RMSEAがやや高く、モデル改善の余地がある可能性があるといえます。
SEM適合指標の基準に関する参考文献
星野 崇宏, 岡田 謙介, 前田 忠彦, 構造方程式モデリングにおける適合度指標とモデル改善について : 展望とシミュレーション研究による新たな知見, 行動計量学, 2005, 32 巻, 2 号, p. 209-235, https://doi.org/10.2333/jbhmk.32.209
◆標準化因子負荷量(Std.all)
・視覚因子 (visual):x1 = 0.77、x2 = 0.42、x3 = 0.58 → x1が最も高い
・言語因子 (textual):x4 = 0.85、x5 = 0.86、x6 = 0.84 → どれも良好
・処理速度 (speed):x7 = 0.57、x8 = 0.72、x9 = 0.67 → x8が最も高い
言語因子(textual)の測定指標は特によく機能しているといえます。
◆潜在因子の相関
・visual ↔ textual:相関 = 0.46
・visual ↔ speed:相関 = 0.47
・textual ↔ speed:相関 = 0.28
各潜在因子間で中程度の相関があるといえます。
※各指標の数値に応じた表現などは、既報などを参照の上、判断されるとよいかと思います。
参考)適合度の数値だけを取り出すには、下記のようなコードでもできます。
fitMeasures(fit, c("chisq", "df", "pvalue", "rmsea", "cfi", "tli"))
# 出力結果 chisq df pvalue rmsea cfi tli 85.306 24.000 0.000 0.092 0.931 0.896
5. パス図の可視化
library(semPlot)
semPaths(
fit,
title = FALSE,
whatLabels = "std", #パス図のラベルを標準化因子負荷量
style = "lisrel",
edge.label.cex = 1.0,
rotation = 2, #図の回転方向の指定
nCharNodes = 0, #ノード名の文字数制限をしない
fade = FALSE,
optimizeLatRes = TRUE,
edge.color = "black",
label.scale = FALSE,
label.cex = 1.0,
theme = 'gray',
node.width = 0.8,
curve = 2, #双方向の相関矢印のカーブの強さ
residScale = 10 #残差(誤差項)の矢印の長さ
)
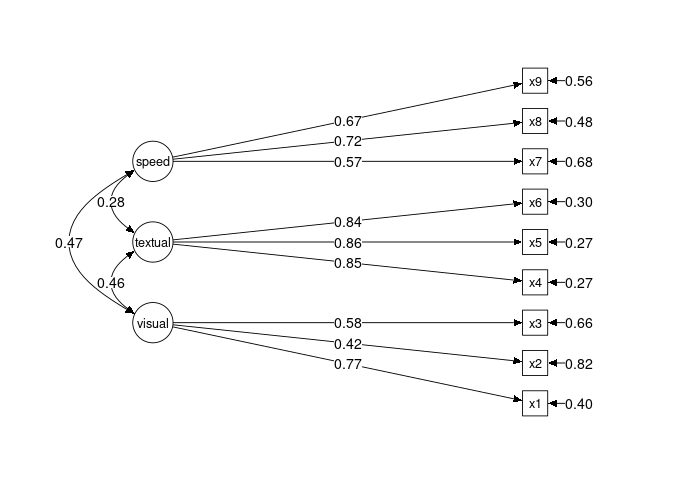
◆ 矢印の意味
・実線の一方向矢印(→)
→ 潜在因子(円) が 観測変数(四角) を説明していることを示します。
例:vsl → x1 は「視覚因子(vsl)が x1 の回答に影響している」ことを意味します。
・両方向の曲線矢印(↔)
→ 潜在因子同士の相関関係を示しています。
例:visual ↔ textual = 0.46 は、視覚因子と言語因子の間に0.46の相関があることを示します。
◆ 数値の意味
・矢印上の数値
→ 標準化因子負荷量(Standardized Loadings)です。0〜1の範囲で、数値が大きいほど関係が強いことを示します。
・四角の右にある数値(例:x1の「0.40」)
→ 各観測変数の誤差分散の大きさを示しています。値が大きいほど誤差が大きいです。
SEMの結果のパス図の可視化を行いました。数値を照らし合わせると、こちらのパス図に記載され、視覚的にも捉えやすくなりました。
semPaths関数での図についてのカスタマイズは以下を参照ください。
semPaths: Plot path diagram for SEM models.
6. まとめ
共分散構造分析(SEM)は、因子分析に加えて、因子同士の関係や誤差項まで含めてモデル化できる柔軟な統計手法です。
今回は、HolzingerSwineford1939データを用いて、「視覚」「言語」「処理速度」という3つの潜在因子に基づいた測定モデルを構築し、SEMでその妥当性を検証しました。
適合度指標(CFI、RMSEA、SRMRなど)に基づいてモデルの当てはまりを評価し、全体としては中程度の適合が得られました。また、標準化因子負荷量やパス図により、各潜在因子がどの観測変数に強く寄与しているかを視覚的にも把握できました。
SEMは、理論に基づいた仮説モデルをデータで検証する分析に適しており、心理・教育・社会学など多くの分野で活用されています。





コメント