主成分分析とは、多くの変数により記述された量的データから、できるだけ少ない情報の損失で、情報を縮約して分析を行う方法です。
多くの変数データを圧縮して2軸、あるいは3軸で分析結果を表示します。
主成分分析は、以下の書籍を参考にされてもよいかと思います。少し昔の発行ですが、たびたび増刷されており、基本がよくわかる書籍です。
◆使用するデータセットについて
今回、Rのdatasetのstate.x77とstate.regionを使用します。
state.x77は、アメリカ合衆国の50州に関するデータセットで、以下の情報が数値で入っています。
Population 人口:1975年7月1日現在の推計人口
Income 所得:一人当たりの所得(1974年)
Illiteracy 非識字率:非識字率(1970年、人口に占める割合
Life Exp 平均寿命(年)(1969-71年)
Murder 殺人:人口10万人当たりの殺人および無過失致死率(1976年)
HS Grad: 高校を卒業した人の割合(1970年)
Frost:首都または大都市で最低気温が氷点下となった日数の平均(1931-1960年)
Area:土地の面積(平方マイル)
state.regionは、各州が所属する地域(northeast北東部、south南部、NorthCentral中北部、west西部)を示します。
state.x77は1930-1970年代の情報で古いため、時代と共に大きく変動があった情報を削除し、PCAを行うこととした。
Population, Life Exp, Frost, Area の4つの情報(因子)を用いてPCAを行います。
help(state.x77) #右下の区画にstate.x77とstate.regionについて記載
head(state.x77) #state.x77の6行目までの情報を確認
Population Income Illiteracy Life Exp Murder HS Grad Frost Area
Alabama 3615 3624 2.1 69.05 15.1 41.3 20 50708
Alaska 365 6315 1.5 69.31 11.3 66.7 152 566432
Arizona 2212 4530 1.8 70.55 7.8 58.1 15 113417
Arkansas 2110 3378 1.9 70.66 10.1 39.9 65 51945
California 21198 5114 1.1 71.71 10.3 62.6 20 156361
Colorado 2541 4884 0.7 72.06 6.8 63.9 166 103766
state.x77_data<-state.x77[,c("Population", "Life Exp","Frost", "Area")] #Population, Life Exp, Frost, Area の4つの情報(因子)を抽出
head(state.x77_data)
Population Life Exp Frost Area
Alabama 3615 69.05 20 50708
Alaska 365 69.31 152 566432
Arizona 2212 70.55 15 113417
Arkansas 2110 70.66 65 51945
California 21198 71.71 20 156361
Colorado 2541 72.06 166 103766
head(state.region) #state.regionの6行目までの情報を確認
[1] South West West South West West
Levels: Northeast South North Central West
state.x77_data_region<-transform(state.x77_data, Region=state.region) #state.x77_dataにstate.regionを列情報として挿入
head(state.x77_data_region) #regionが列情報として挿入されたことを確認
Population Life.Exp Frost Area Region
Alabama 3615 69.05 20 50708 South
Alaska 365 69.31 152 566432 West
Arizona 2212 70.55 15 113417 West
Arkansas 2110 70.66 65 51945 South
California 21198 71.71 20 156361 West
Colorado 2541 72.06 166 103766 West
各州に関して抽出した情報(state.x77_data)と、各州が所属する地域の情報(state.region)を合わせたデータ(state.x77_data_region)を作成しました。
これにより、各州の抽出情報から得られた分布と、地域属性がどのように関わるかを見ることができます。
この合わせたデータ(state.x77_data_region)を用いて、主成分分析を行っていきます。
◆主成分分析
主成分分析(PCA)結果をbiplot、2軸の図にプロットを行います。
biplotは、PCAでサンプルがどのように関連しているか(どのサンプルが似ていて、どのサンプルが違うか)を可視化し、同時に各変数が各主成分にどのように寄与しているかを明らかにする手法です。
パッケージは、ggbiplotを用いて行っていきます。
まずは、インストールから。
#ggbiplotパッケージのインストール・ライブラリー
library(devtools)
install_github("vqv/ggbiplot") #これでfailedになる方は、次を試してください。 install.packages("remotes") remotes::install_github("vqv/ggbiplot") library(ggbiplot)
これでggbiplotがインストールできました。
PCAを作成し、表示していきます。
state.x77_data_region.pca <- prcomp(state.x77_data_region[,c(1:4)], center = TRUE,scale. = TRUE)
ggbiplot(state.x77_data_region.pca) #①biplotで視覚化
ggbiplot(state.x77_data_region.pca, labels=rownames(state.x77_data_region))+theme_bw() #②①+各プロットに州の名前を入れて、背景白にする
ggbiplot(state.x77_data_region.pca,ellipse=TRUE, labels=rownames(state.x77_data_region), groups=state.x77_data_region$Region)+theme_bw()+xlim(-2.5,3) #③②+グループによる色分け+図の軸目盛設定(x軸)
ggbiplot(state.x77_data_region.pca,ellipse=TRUE,choices=c(3,4), labels=rownames(state.x77_data_region), groups=state.x77_data_region$Region)+theme_bw() #④③をPC3とPC4の2軸で表す
prcomp(state.x77_data_region[,c(1:4)], center = TRUE,scale. = TRUE)
prcompがPCAを実施するコードで、state.x77_data_regionの[,c(1:4)]は、2列目(Polution)から5列目(Area)までのデータを用いるという意味。
#① biplotで視覚化
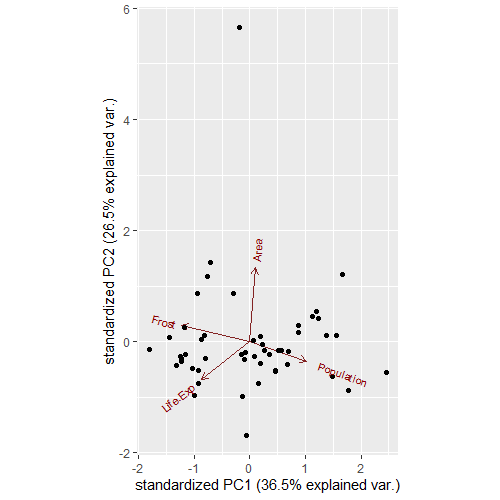
中心点から矢印が示されていますが、各変数が各軸に寄与する方向を示しております。
例えば,変数Populationは PC1の正の方向に、FrostはPC1の負の方向に寄与しており,この変数の値が正に大きいほど,右にプロットされています。
#②①+各プロットに州の名前を入れて、背景を白くしました。
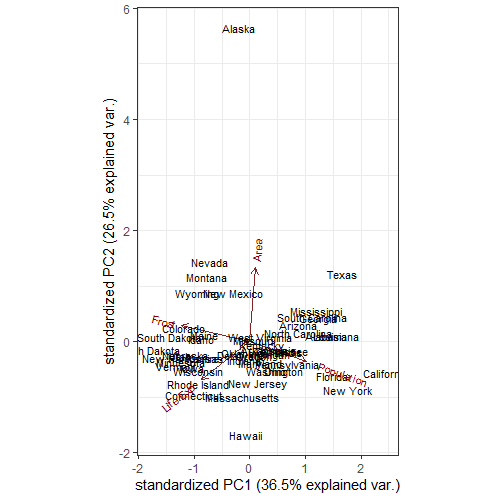
+theme_bw()は、ggplot2でも一度やっていますが、いろいろと背景を変更されたい必要な方はこちらも参考考にされてください。
#③②+グループによる色分け+図の軸目盛設定(x軸)
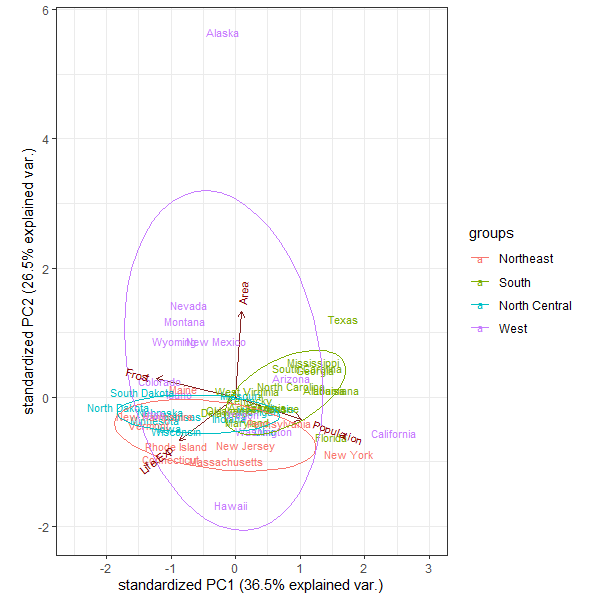
ellipse=TRUEを設定すると、各グループを囲むように楕円が描かれます。
+xlim(-2.5,2.5)で、目盛を指定しました。なお、y軸を設定したい場合は、+ylim(下限 , 上限 )を入れてください。
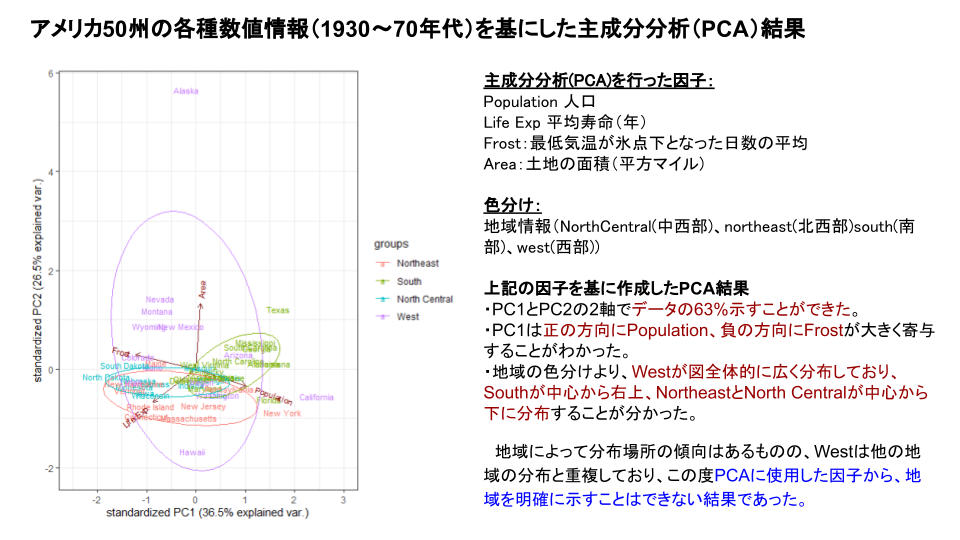
PC1がデータ全体の36.5%を説明できており, PC2が26.5%であるので、PC1とPC2の2軸でデータの63%を説明できる結果でした。
また、地域による色分けでは、Westが図全体的に広く分布しており、Southが中心から右上、NortheastとNorth Centralが中心から下に分布した結果でした。
地域によって分布場所の傾向はあるものの、Westは広く分布しており、重複しており、この度使用した因子では、地域の特性を明確に示すことはできない結果となりました。
#④③をPC3とPC4の2軸で表す
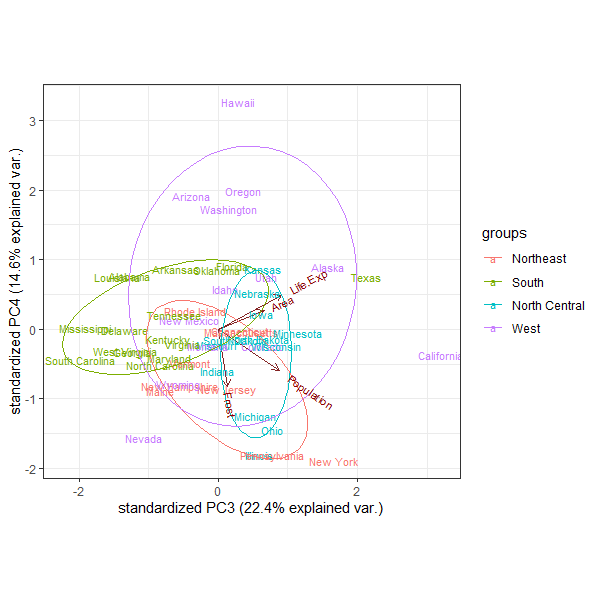
ggbiplotの中でchoices=c(3,4)と指定することで、PC3とPC4を軸としたプロットを表示することができます。
◆プレゼンテーション


コメント