Rでメタアナリシス①　ー効果量, リスク比, 効果モデルの選択, metaforー

メタアナリシスは、論文などで報告された同じテーマに関する複数の研究結果を統合する統計学的手法です。
重要なデータを多く組み合わせて議論することから、質の高いエビデンスレベルであるとされています。
臨床試験（治療の有効性や安全性など）結果、例えば、特定治療法の効果を統合することで治療法の総合的な効果を把握することなどで広く使われています。

■目次
1.　メタアナリシスの流れ
2.　メタアナリシス用データセットの紹介ーmetaforパッケージー
3.　メタアナリシス ―相対リスク（RR）の推定, 固定効果モデル, ランダム効果モデル, 平均リスク比―
4.　メタアナリシス ―metafor, フォレスト図ー

1.　メタアナリシスの流れ

実際、メタアナリシスを進める大まかな流れについて、以下に記載します。
①文献の収集: 対象となる研究や試験の文献収集。対象サイト（PubMed, MEDLINE, Google Scholarなど）や検索式、検索日、対象期間などは、研究の再現性の観点から記載は重要です。
②文献の選択: 収集された文献について、適格基準（研究デザイン、対象者、アウトカムなど）と除外基準に沿って選定を行う。
③データの抽出: 選定された文献からデータを抽出し、同一形式でまとめる。
④データの統合: 効果モデル（固定効果モデル or ランダム効果モデル）を用いて効果量（効果サイズ, エフェクトサイズ）の統合を行う。
⑤異質性の評価: 研究間の異質性を評価(Q統計量、I^2統計量など)し、結果の一貫性を確認する。
⑥出版バイアスの評価:ファンネルプロット、Eggerテスト、Beggテストなどで出版バイアスを検出。
⑦メタ回帰やサブグループ分析: 必要に応じて、異なる要因や条件に基づいて結果を詳細に分析する。

PRISMA声明（https://www.prisma-statement.org/）にメタアナリシスのチェック項目やフローなどがありますので、参考にされてください。

ここでは、①～③が完了し、まとめたデータについて「④データの統合」以降のRでの解析手順を解説していきます。

2.　メタアナリシス用データセットの紹介ーmetaforパッケージー

Rのmetaforパッケージ内には、メタアナリシスのながれ「④データの統合」以降に使用できるデータセットが複数登録されており、今回はそのうち二つを紹介します。

install.packages("metafor")
library(metafor)
dat.bcg #1
#   trial               author year tpos  tneg cpos  cneg ablat      alloc
#1      1              Aronson 1948    4   119   11   128    44     random
#2      2     Ferguson & Simes 1949    6   300   29   274    55     random
#3      3      Rosenthal et al 1960    3   228   11   209    42     random
#4      4    Hart & Sutherland 1977   62 13536  248 12619    52     random
#5      5 Frimodt-Moller et al 1973   33  5036   47  5761    13  alternate
#6      6      Stein & Aronson 1953  180  1361  372  1079    44  alternate
#7      7     Vandiviere et al 1973    8  2537   10   619    19     random
#8      8           TPT Madras 1980  505 87886  499 87892    13     random
#9      9     Coetzee & Berjak 1968   29  7470   45  7232    27     random
#10    10      Rosenthal et al 1961   17  1699   65  1600    42 systematic
#11    11       Comstock et al 1974  186 50448  141 27197    18 systematic
#12    12   Comstock & Webster 1969    5  2493    3  2338    33 systematic
#13    13       Comstock et al 1976   27 16886   29 17825    33 systematic

#1 dat.bcg ←データセット例としてよく使われています。
Studies on the Effectiveness of the BCG Vaccine Against Tuberculosis
結核に対するBCGワクチンの有効性に関する研究（13の研究結果のデータ）
author　著者名
year　発表年
tpos （ワクチン接種）群における結核陽性症例数
tneg （ワクチン接種）群における結核陰性症例数
cpos　コントロール（ワクチン非接種）群における結核陽性症例数
cneg　コントロール（ワクチン非接種）群における結核陰性症例数
ablat　試験地の絶対緯度（度）
alloc　治療割り付け方法（ランダム、交互、システマティックレビュー）

こちらのデータは、著者名、発表年、陽性や陰性の患者数などをまとめていることが分かります。

dat.laopaiboon2015 #2
#      author year ai n1i ci n2i      age diag.ab diag.cb diag.pn        ctrl
#1     Balmes 1991  4  48  7  56   adults       1       0       0   amoxyclav
#2      Beghi 1995 22  69  2  73   adults       0       1       0   amoxyclav
#3   Biebuyck 1996 53 497 53 257   adults       1       1       0   amoxyclav
#4     Daniel 1991  5 121 10 120   adults       1       0       0 amoxycillin
#5   Ferwerda 2001  5  55  7  53 children       0       0       1   amoxyclav
#6       Gris 1996  6  34  2  33   adults       1       1       1   amoxyclav
#7     Harris 1998 11 125  4  63 children       0       0       1   amoxyclav
#8  Hoepelman 1993  4  48  4  51   adults       1       0       0   amoxyclav
#9  Hoepelman 1998  3  62  5  61   adults       0       1       0   amoxyclav
#10   Mertens 1992  1  25  5  25   adults       0       1       0 amoxycillin
#11   Sevieri 1993  5  25  2  25   adults       0       1       0   amoxyclav
#12  Whitlock 1995  0  29  2  27   adults       0       1       0   amoxyclav
#13    Wubbel 1999  1  39  2  49 children       0       0       1   amoxyclav
#14 Zachariah 1996  8 173  7 173   adults       1       1       1   amoxyclav
#15     Zheng 2002 12  38  2  42   adults       0       1       0   amoxyclav

#2 dat.laopaiboon2015
Studies on the Effectiveness of Azithromycin for Treating Lower Respiratory Tract Infections
下気道感染症に対するアジスロマイシンの有効性に関する研究(15の研究結果のデータ)
author　著者名
year　発表年
ai　アジスロマイシンを投与した群における臨床的失敗例数
n1i　アジスロマイシン投与群における患者数
ci　アモキシシリンまたはアモキシクラブを投与した群における臨床失敗例数
n2i　アモキシシリンまたはアモキシクラブを投与した群における患者数
age　試験の対象が成人か小児か
diag.ab　急性細菌性気管支炎と診断された患者を含む試験（0/1：含まない/含む）
diag.cb　急性増悪を伴う慢性気管支炎と診断された患者を含む試験（0/1：含まない/含む）
diag.pn　肺炎と診断された患者を含む（0/1：含まない/含む）
ctrl　対照群の抗生物質（アモキシシリンまたはアモキシクラブ）

こちらのデータは、著者名、発表年、患者総数や失敗例数などの情報をまとめていることが分かります。

今回は dat.laopaiboon2015のデータを使用して解析を進めます。

3.　メタアナリシス ―リスク比（RR）の推定, 効果モデルの選択, 平均リスク比―

「④データの統合」と「⑤異質性の評価」を進めます。
効果量の選択について、dat.laopaiboon2015のデータは、イベント発生の有無、つまり2値のデータですので、リスク比 (相対リスク, RR) とオッズ比 (OR)を効果量の候補として検討します。
効果量の選択は、研究の目的やデータの特性によって異なります。

今回は発生確率の比を解釈するためリスク比を選択して、進めます。
近年のメタアナリシスではオッズ比を選択されることも多いです。
これらの違いについては、別の機会に解説をしたいと思います。

上記のdat.laopaiboon2015を使用して、メタアナリシスを行います。

ai, n1i, ci, n2i は、2×2分割表（カテゴリカルデータを2つの軸で整理した値）を表しています：
群　　　　失敗例数　患者数
投与群　　ai　　　　n1i
非投与群　ci　　　　n2i

効果モデルの選択について検討します。
・固定効果モデル：　すべての研究が同一の「真の効果」を測定していると仮定しており、統合して得られる母集団の推定値が一つであると考える。異質性が低い場合に適しており、高い場合は適さない。
・ランダム効果モデル：　各研究が異なる「真の効果」をもつ可能性があると仮定し、研究間の異質性が考慮され、効果量の分布の平均を推定する。異質性が高い場合でも使用できるが、非常に大きい場合は慎重な解釈が必要。

二つの効果モデルは、異質性に対するアプローチが異なります。異質性を判断基準とされることも多く、I^2>50%の場合、ランダム効果モデルを選択されることが多いです。
まずは、異質性を確認するため、固定効果モデルとして異質性の計算も含めてRRの推定に関するコードを走らせます。

固定効果モデルを計算する際の手法を選択できます。
・Mantel-Haenszel法（MH）：2×2分割表で効果量を計算する。異質性が小さい場合に適用される。
・Inverse Variance法（IV）：分散の逆数を重み付け。精度の異なる研究を統合する際に使用される。
・Peto法：稀なイベントのオッズ比を推定する際に使用される。

今回は、MH法を用いて固定効果モデルの計算を行います。

dat <- dat.laopaiboon2015
rma.mh(measure="RR", ai=ai, n1i=n1i, ci=ci, n2i=n2i, data=dat, digits=3) 　#3 固定効果モデル（Mantel-Haenszel法）による相対リスク（RR）の推定
#Equal-Effects Model (k = 15)
#I^2 (total heterogeneity / total variability):  65.30%　　# 合計異質性
#H^2 (total variability / sampling variability): 2.88　　# 合計の変動をサンプリング変動で割ったもの
#Test for Heterogeneity:   # 異質性の検定結果
#Q(df = 14) = 40.348, p-val < .001  # p値は0.001未満であり、異質性が存在する
#Model Results (log scale):
#estimate     se    zval   pval   ci.lb  ci.ub 
#  -0.083  0.117  -0.709  0.479  -0.311  0.146 
#Model Results (RR scale):
#estimate  ci.lb  ci.ub 
#   0.921  0.733  1.157   # 相対リスクの推定値

#3　MH法を用いた固定効果モデルにおいて、相対リスク（RR）などの効果サイズの計算
aiは投与群のイベント数、n1iは投与群の総患者数、ciは非投与群のイベント数、n2iは非投与群の総患者数。digitsは有効数字の指定。

このメタアナリシスではMH法を用い固定効果モデルの相対リスク（RR）を推定しました。
異質性の評価によると、I^2は65.30%で、相当な異質性があることが分かりました。
※異質性の判断基準（参考Website　Cochrane Handbook（https://training.cochrane.org/handbook））
0～40％重要でない異質性
30～60％中程度の異質性
50～90％相当な異質性
75～100％高度の異質性

Equal-Effectsモデルによる分析では、全体の変動に占める異質性の割合（H^2）は2.88です。異質性の検定（Q統計量）も有意で、p値は0.001未満です。

今回、異質性I^2>50%でしたので、ランダム効果モデルを選択し、効果量の統合を進めていきます。

ランダム効果モデルを計算する際の手法を選択できます。
・Restricted Maximum Likelihood（REML法）：最尤法（ML）の拡張版で、異質性を推定する。
・DerSimonian and Laird（DL法）：Cochran’s Q統計量を基に異質性の分散を推定する。
・Maximum Likelihood（ML）：モデル全体の尤度を最大化する方法で、異質性を直接推定。

今回は、REML法を選択し、計算を進めます。

res<-rma(measure="RR", ai=ai, n1i=n1i, ci=ci, n2i=n2i, data=dat, method="REML")#4 RRのランダム効果モデル（REML法）
res
#Random-Effects Model (k = 15; tau^2 estimator: REML)
#tau^2 (estimated amount of total heterogeneity): 0.5874 (SE = 0.3897)　#推定された総異質性の量
#tau (square root of estimated tau^2 value):      0.7664　#推定された tau^2 の平方根
#I^2 (total heterogeneity / total variability):   64.85%　#総異質性の割合
#H^2 (total variability / sampling variability):  2.84　#全変動と抽出変動の比率
#Test for Heterogeneity: 
#Q(df = 14) = 38.4438, p-val = 0.0004  #異質性の検定統計量
#Model Results:
#estimate      se    zval    pval    ci.lb   ci.ub    
#  0.0852  0.2673  0.3186  0.7501  -0.4388  0.6092    
#---
#Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

predict(res, transf=exp) #5 95% CI付き平均リスク比
#   pred  ci.lb  ci.ub  pi.lb  pi.ub 
# 1.0889 0.6448 1.8389 0.2218 5.3447

#4 ランダム効果モデル
こちらのモデルでの総異質性の割合（I^2）が64.85%と高いことを示しています。
ランダム効果モデルの tau^2 推定値は0.5874で、異なる研究間での効果のばらつきが大きいことを示唆しています。
異質性の検定も有意であり、真の効果が均一ではない可能性があります。
対数リスク比の推定値は0.0852で、統計的に有意ではありません（p値 = 0.7501）。
信頼区間（CI）も-0.4388から0.6092まで幅広く、真の効果の位置が確定しづらいことを示しています。
異質性があるため、結果の一般化に注意が必要であり、個々の研究の特性を考慮した解釈が必要です。

#5　平均リスク比
メタアナリシスの結果から算出されたランダム効果モデルにおける平均リスク比（Risk Ratio, RR）を指数変換して、元のスケールに戻しています。
具体的には、元スケールで相対リスク（RR）の推定値を得ています。
pred：平均リスク比の推定値
ci.lb/ci.ub： 95%信頼区間の下限 / 95%信頼区間の上限
pi.lb/pi.ub： 95%予測区間の下限 / 95%予測区間の上限

平均リスク比が1.0889であり、投与群のリスクが非投与群に比べてわずかに高いことを示しました。
信頼区間が0.6448～1.8389であり、１が含まれているため、投与による有意な効果があるとは言い切れない結果でした。
また、予測区間においても、0.2218～5.3447で信頼区間よりも広く、研究の異質性が大きいことが分かりました。

4.　メタアナリシス ―metafor, フォレスト図ー

フォレスト図は、異なる研究の効果サイズやその信頼区間を視覚的に表現するメタアナリシスの結果の図です。
各研究の点と線で示し、全体の効果サイズを中心に配置され、信頼区間が表示されます。
3.の#4 RRのランダム効果モデル（REML法）の結果をフォレスト図で表します。

forest(res, header="Author, Year", slab=paste(dat$author, dat$year, sep=", "), showweights=TRUE, atransf = exp,at = log(c(0.001,0.01, 0.1, 1, 10, 100))) #フォレスト図

#6　フォレスト図
atransf = exp　で効果量が対数スケールで計算されていたのを、元スケールで表示します。
図の左から、研究の著者および発表年、エラーバー95%信頼区間、研究がメタアナリシス全体に占めるウェイト（重み）の割合（標本サイズに基づいて計算）、効果量RRの推定値[95％信頼区間]を示しています。

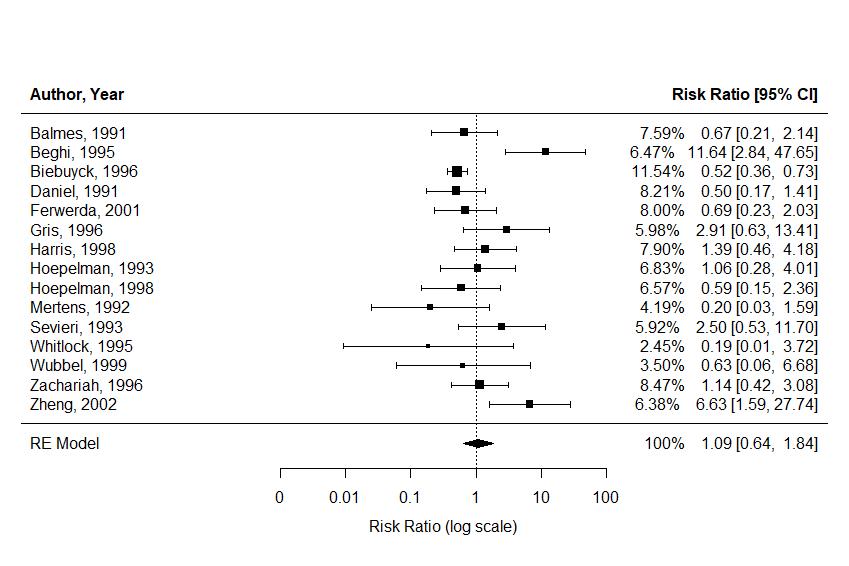
3.のランダム効果モデルの結果をフォレスト図にすることによって、視覚的に捉えやすくなりました。

メタアナリシスにおける出版バイアスについてのRでの解説記事がありますので、参考にしていただけますと幸いです。