1. 研究の背景と目的
近年のAlphaFold 21/32の登場は、タンパク質の「静的な3D構造」の高精度予測を可能にしました。しかし、タンパク質の機能は、その動き、すなわち「ダイナミクス」とも密接に関連しています。AlphaFoldの成功から、「その構造のダイナミクスの予測」という段階に進むのは自然な流れです。
タンパク質の動きは、古典的分子動力学(MD)によりシミュレーションすることができます。しかし、MDシミュレーションは、生命現象の理解に必要なミリ秒以上のタイムスケールをカバーするには、莫大な計算を必要とするという問題を抱えています。
この「ポストAlphaFold時代」の課題解決のために、拡散モデル等の生成AIを利用しようとする試みが進んでいます。本稿で取り上げるPTraj-Diff (Protein Trajectory diffusion) もその1つです。
PTraj-Diff paper:Xu K, et al. (2025) Efficient Generation of Protein and Protein-Protein Complex Dynamics via SE(3)-Parameterized Diffusion Models. J Chem Inf Model. Preprint, doi: 10.1021/acs.jcim.5c01971.
PTraj-Diff Guthub:PTraj-Diff https://github.com/lfs119/PTraj-Diff
PTraj-Diffは、MDシミュレーションを完全に置き換えることではなく、比較的短時間のMDトラジェクトリから「結果(平衡コンフォメーションの分布)」を学習し、タイムスケールの限界を超える「平衡コンフォメーションのサンプリングを加速する」ことを実現しています。
2. PTraj-Diffのメソッド、および関連コード
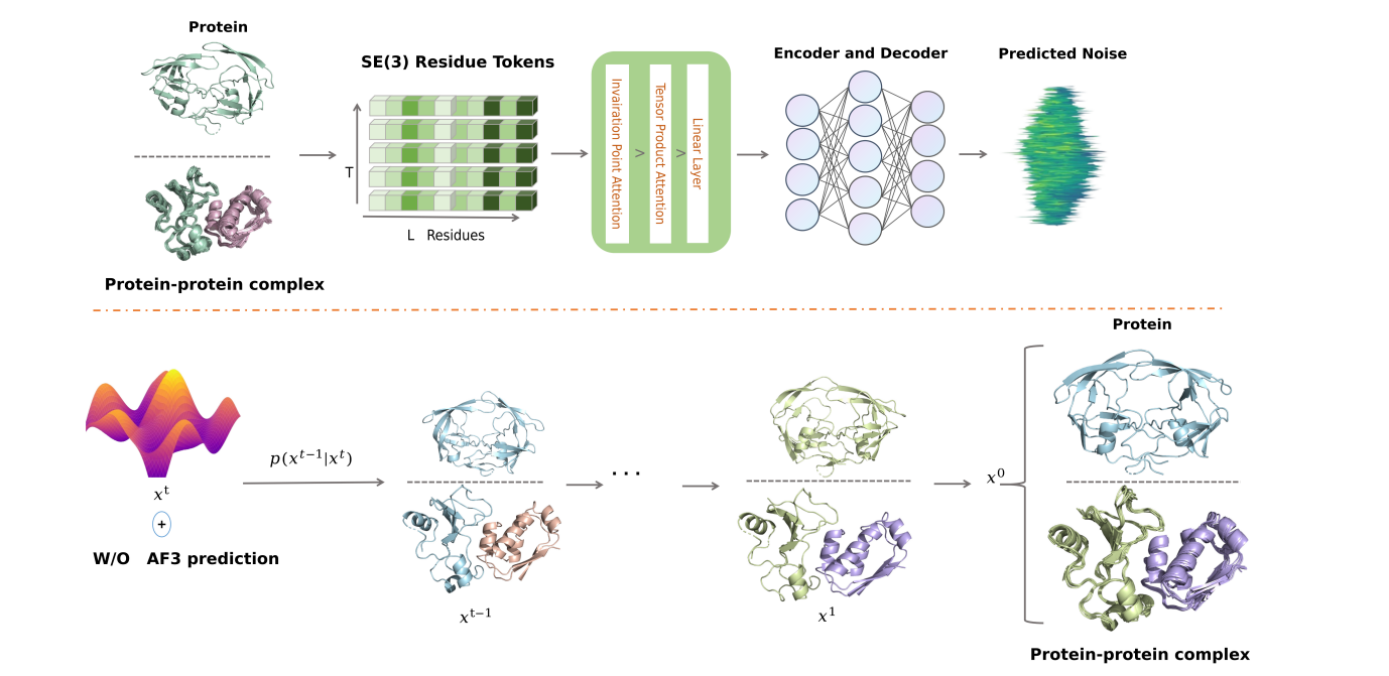
「静的な構造の集団(アンサンブル)」の生成に留まらず、「時間的な連続性を持つトラジェクトリ」を生成できなければ、タンパク質がどのように状態遷移するか、その速度はどれくらいかといった、機能解明に不可欠なマルコフダイナミクスの解析を行うことはできません。PTraj-Diffは、この限界を克服するために設計た生成AIです。
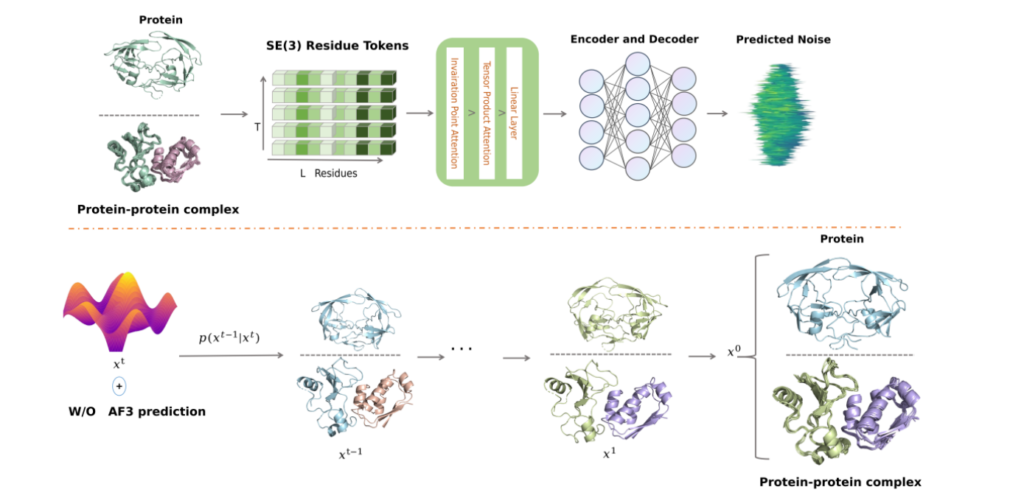
この「連続的トラジェクトリ」の生成というタスクを実現するため、PTraj-Diffは複数の技術要素を組み合わせています。その論文と公開リポジトリを検討しました。
2.1 PTraj-Diffの核心(1): SE(3) パラメータ化
PTraj-Diffの学習データは、古典的MDシミュレーションによって生成されたトラジェクトリ(時系列)データです。2つのタンパク質複合体(Barnase-Barstar [PDB: 1BRS] と HIV-1 Protease [PDB: 1HPV])が用いられ、MD計算には、OpenMM3 と AMBER4 が使用されています。
OpenMMについては、Hira Laboでもいくつか記事を書いてますので、ご参考まで。
原子座標時系列データを効率的に学習し、生成能力を獲得するためには、幾何学的表現の標準化が不可欠となります。PTraj-Diffは、タンパク質の物理的対称性(剛体運動に対する不変性)を遵守するため、その構造を残基レベルのSE(3)変換を用いて記述します。SE(3)(特殊ユークリッド群)は、3次元空間における剛体運動、すなわち回転(SO(3))と並進(R3)を記述する数学的な枠組みです。
このデータ表現は、先行研究であるMDGen5と同じパラメータ化を採用しており、これは全原子トラジェクトリをSE(3)不変なトークンの時系列として扱います。PTraj-DiffにおけるSE(3)パラメータ化の実装は、主に幾何学的基盤の定義、構造定数の定義、座標変換ロジックの3つのファイルとクラスが連携することで実現されています。
2.2 PTraj-Diffの核心(2): 拡散ベース生成
PTraj-Diffは生成エンジンとして拡散モデルを採用しており、先述の核心(1)で作成したSE(3)トークン配列を学習します。拡散生成は、ノイズスケジュールの定義、単一ステップのノイズ除去、およびサンプリングループの3要素で構成されます。
・学習方法
ー 順プロセス(Forward Process):トラジェクトリを「壊す」 まず、SE(3)トークン配列(元の安定な構造 X0)に、プログラムが意図的にノイズを少しずつ加えていき(add noise)、最終的に完全なランダムノイズ(Xt)の状態にします。
ー 逆プロセス(Reverse Process):トラジェクトリを「復元」させる モデルには、「ノイズが加えられた途中の状態」のトラジェクトリが入力されます。モデルは、「元の状態に戻すために、どのようなノイズが加えられたか」を予測します。この「ノイズ除去」(denoise)の訓練を何千エポックも(論文では10,000エポック)繰り返すことで、モデルは「ノイズだらけの状態」から「物理的に妥当な状態」へと戻す手順を学習します。
・ノイズ(ベータ)スケジュールの定義と計算
訓練には二次分散スケジュールが採用されています。diff/beta_schedules.pyにて、シグモイド関数を用いたベータ値の生成と、逆拡散に必要なアルファ値(α)の導出を行います。
def quadratic_beta_schedule(
timesteps: int, beta_start=1e-4, beta_end=0.02
) -> torch.Tensor:
betas = torch.linspace(-6, 6, timesteps)
return torch.sigmoid(betas) * (beta_end - beta_start) + beta_start
def compute_alphas(betas: torch.Tensor) -> Dict[str, torch.Tensor]:
alphas = 1.0 - betas
alphas_cumprod = torch.cumprod(alphas, dim=0)
# ... (sqrt_alphas_cumprodなどの計算)
return { "betas": betas, "alphas": alphas, "alphas_cumprod": alphas_cumprod, ... }・単一タイムステップのノイズ除去 (p_sample)
diff/sampling.pyのp_sampleは、単一ステップのデノイズを実行します。学習済みモデル(ノイズ予測器)の出力を利用し、ノイズ除去後の平均構造(model_mean)を推定します。
@torch.no_grad()
def p_sample(model: nn.Module, x: torch.Tensor, t: torch.Tensor, ..., betas: torch.Tensor, prep) -> torch.Tensor:
# Equation 11 in the paper
# model(x, t, ...) は、ノイズ予測器(BERTエンコーダ)の呼び出し
model_mean = sqrt_recip_alphas_t * (
x - betas_t * model(x, t, mask=prep['model_kwargs']["mask"], ...) / sqrt_one_minus_alphas_cumprod_t
)
if t_index == 0:
return model_mean
else:
# ノイズを加えて次のステップのサンプリング
noise = torch.randn_like(x)
return model_mean + torch.sqrt(posterior_variance_t) * noise・サンプリングループの管理 (p_sample_loop)
p_sample_loopは、p_sampleを逆向き(T → 0)に繰り返し呼び出すことで、ランダムノイズから最終的なタンパク質軌跡データ(剛体変換やねじれ角)を生成します。
@torch.no_grad()
def p_sample_loop(model: nn.Module, ..., timesteps: int, betas: torch.Tensor, prep) -> torch.Tensor:
# ... (ノイズ x から開始)
for i in tqdm(
reversed(range(0, timesteps)), # 逆向きにループを実行
desc="sampling loop time step",
total=timesteps,
):
img = p_sample(
model=model,
x=img,
t=torch.full((b,), i, device=device, dtype=torch.long), # 時間 t を渡す
betas=betas,
prep=prep,
)
return img2.3 PTraj-Diffの核心(3): 時間的依存性のモデル化(BERT)
PTraj-Diffは、空間的な処理(SE(3)やIPA/TPA)と時間的な処理(BERT)を融合させています。トラジェクトリという「時系列データ」における長距離の時間的依存性を捉えるためにBERTが用いられており 、これにより時間的に連続した軌道の生成が可能になるとのことです。トラジェクトリの時間的依存性を学習する鍵は、連続的な幾何学的特徴量の埋め込み、時間情報の注入、およびシーケンス化の3点に集約されます 。
・実装の主要ファイル(diff/modelling.py)
モデルの核となるBertForDiffusionBaseクラスは、位置・時間埋め込み層とBERTエンコーダを保持します。拡散モデルのタイムステップ(timestep)情報を埋め込みベクトルに変換し、入力シーケンスに加算する処理もここに含まれます。これにより、モデルは「今どのノイズレベルの処理をしているか」を認識できます。
2.4 PTraj-Diffの核心(4): 幾何学的アテンション(IPA / TPA)
PTraj-Diffモデルの独自性として、IPAレイヤー内で従来のMulti-Head Attention (MHA) の代わりに Tensor Product Attention (TPA) を導入しています 。論文によれば、TPAの採用によりIPAブロックの訓練に必要なパラメータ数が「約1/6に削減」され、計算コストとハードウェア要件が劇的に低減されています 。
・IPA層(IPALayer)の統合構造
diff/modelling.pyで定義されるIPALayerは、時間埋め込み(t)によるAdaLN変調下で、幾何学的処理とシーケンス処理を統合します 。
def forward(self, x, t, mask=None, frames=None):
# ... (AdaLN modulation by time t) ...
# 1. Invariant Point Attention (IPA)の適用
x = x + self.ipa(self.ipa_norm(x), frames, frame_mask=mask)
residual = x
# 2. Tensor Product Attention (TPA) の適用 (MHAの代わり)
x = modulate(self.mha_layer_norm(x), shift_msa_l, scale_msa_l)
x = self.mha_l(x, mask=mask)
x = residual + gate_msa_l.unsqueeze(1) * x
# ... (Feed-Forward Network) ...
return xここでself.ipaは幾何学的特徴を更新し、続くself.mha_l(TPA)が長距離依存性を効率的に学習します。
・IPAにおける剛体変換(SE(3)不変性)の利用
IPA(diff/ipa.py)は、剛体変換Rigid(diff/rigid_utils.py)を用いて座標変換を行い、SE(3)不変性を保証します 。
# [*, N_res, H * P_q * 3]
q_pts = self.linear_q_points(s)
# ... (shape manipulation) ...
# 剛体変換 r を使ってクエリ点 q_pts をグローバル座標系に適用
q_pts = r[..., None].apply(q_pts)
# 同様にキー点 k_pts, バリュー点 v_pts もグローバル座標系に変換
# ... (kv_pts calculation and application of r) ...
# [*, N_res, N_res, H, P_q, 3]
# グローバル座標系での点特徴の距離二乗を計算し、アテンションスコアに組み込む
pt_att = q_pts.unsqueeze(-4) - k_pts.unsqueeze(-5)
pt_att = pt_att**2各残基の点特徴に剛体変換rを適用(.apply())してグローバル座標へ移し、その距離(pt_att)に基づいてアテンションを計算することで、空間配置に依存しない幾何学的関係を捉えます。
・TPA(Tensor Product Attention)による効率化
TPA(diff/modelling.py)は、低ランク近似によりMHAの計算コストを劇的に削減します 。
class TPA(nn.Module):
def __init__(self, d_model, n_heads, rank_ratio=0.25):
# ... (initialization) ...
self.rank = max(n_heads, int(d_model * rank_ratio))
self.rank_per_head = self.rank // n_heads
# 低ランクでのQ/K/V変換
self.Wq = nn.Linear(d_model, self.rank, bias=False)
self.Wk = nn.Linear(d_model, self.rank, bias=False)
self.Wv = nn.Linear(d_model, self.rank, bias=False)
# テンソル積による高次元への復元を制御するパラメータ
self.U = nn.Parameter(torch.Tensor(n_heads, self.head_dim, self.rank_per_head))
self.V = nn.Parameter(torch.Tensor(n_heads, self.rank_per_head, self.head_dim))隠れ次元d_modelより低いランクで計算を行うこの構造が、高精度な動態生成を低リソースで実現する基盤となっています。
3. リザルト:高品質かつ長時間のトラジェクトリ生成
これらのメソッドを組み合わせた結果、PTraj-Diffは高品質なトラジェクトリを生成できることが示されています。
1. 静的品質: 生成された個々の構造は、単量体(1HPV)でTM-Score 100%(高品質範囲内)、複合体(1BRS)でDockQ 96%(Excellentレンジ、data8)と、非常に高品質です。
2. 分布の忠実性: 生成された構造の「集団」は、ラマチャンドランプロットにおいて、学習データであるMDシミュレーションの結果と高い一致を示しました。
3. マルコフ特性: PTraj-Diffが「連続的トラジェクトリ」を生成できる証拠として、マルコフ状態モデル(MSM)分析が行われました。その結果、単量体(1HPV)は多様な状態間を柔軟に遷移する特性を、複合体(1BRS)は特定の安定状態に強く収束する安定した特性を示し、系に応じた異なるマルコフ遷移を生成することが示されました。
4. 長時間生成とAlphaFold3連携: 学習時(例:60フレーム)より大幅に長いタイムステップ(例:3000フレーム)での生成や、学習データ(1usまで)に含まれない未来のトラジェクトリ(1us以降)の生成評価が行われました。さらに、AlphaFold3が予測した学習データ外の静的構造を初期構造として入力しても、高品質なトラジェクトリ(TM-Score 100%, DockQ 99%以上)を安定して生成できることが示されました。
4. まとめと将来展望
MDGen5などの先行研究と同様、PTraj-DiffはMDシミュレーションの結果を学習し、トラジェクトリ生成できることを示しました。これらの生成AIは、タンパク質の動的性質を予測可能であり、生成AIによる大きな進歩です。一方で、論文の著者自身が「結論」の章で、その明確な限界点を率直に認めています。
AlphaFold3の登場で、「タンパク質-リガンド(低分子化合物)」の結合構造を高精度で予測可能になりました。しかし、現状のトラジェクトリ生成AIは「タンパク質-リガンド複合体」に適用できず、今後の課題です。
参考文献
1. Jumper, J. et al. (2021). Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589 doi:10.1038/s41586-021-03819-2
2. Abramson, J. et al. (2024) Accurate structure prediction of biomolecular interactions with AlphaFold 3. Nature 630, 493–500. doi: 10.1038/s41586-024-07487-w
3. Eastman, P. et al. (2017) OpenMM 7: Rapid development of high performance algorithms for molecular dynamics. PLOS Computational Biology 13(7): e1005659. doi: 10.1371/journal.pcbi.1005659
4. Weiner, P. K., Kollman, P. A. (1981) AMBER: Assisted model building with energy refinement. A general program for modeling molecules and their interactions. J. Comput. Chem. 2, 287–303, doi: 10.1002/jcc.540020311
5. Jing, B. et al. (2024). Generative Modeling of Molecular Dynamics Trajectories. arXiv:2409.17808 doi: 10.48550/arXiv.2409.17808



コメント