「この患者さんは、病気を発症するリスクが高いか?」
「どういった特徴を持つ人が保険を解約するか?」
私たちの周りには、物事を分類したり、将来を予測したり、といった場面がたくさんあります。これまでの記事では、数値(例:住宅価格)を予測する重回帰分析や、ある事象が起こる「確率」を計算して「はい/いいえ」といった二値の予測・分類を行うロジスティック回帰(基本編、正則化編)などを学んできました。ロジスティック回帰は、統計的なモデルに基づいて分類を行いましたね。
今回は、それらとは異なる視点から分類を行う決定木について、Rのコードと共に解説します。
決定木は、二値分類だけでなく、複数のグループへの分類にも柔軟に対応できる手法です。ロジスティック回帰が確率的なアプローチを取るのに対し、決定木は「もしAという条件ならX群、もしBという条件ならY群」といった具体的なルールを木の枝のように見つけていくことでデータを分類します。まるで「はい/いいえ」で進むフローチャートのようなモデルで、その判断プロセスが目で見て分かりやすいことから、機械学習の入門としても人気があります。
1. 決定木とは
2. 使用パッケージとデータ
3. Rで決定木モデルの構築と可視化
3-1. パッケージのインストールと読み込み
3-2. 学習データとテストデータへの分割
3-3. 決定木モデルの構築
4. モデルの性能評価
5. まとめ
1. 決定木とは
機械学習とは、大量のデータを読み込ませて、その中に潜むパターンやルールを自動的に見つけ出す技術です。見つけ出したパターンを使って、新しいデータに対する予測や分類を行います。
その代表的な手法の一つが決定木(Decision Tree)です。
決定木は、データが持つ特徴(説明変数)について、最もよく分離できる質問を繰り返します。
例えば、「この動物は何?」という分類をしたい場合、
よく分離できる質問として「羽があるか?」という質問を見つけ出し、これをスタートとして、その答えに応じて「空を飛べるか?」や「足が4本あるか?」といった質問を見つけ出し、分類していきます。
このように、木が枝分かれするように判断を繰り返すことで、最終的にデータをいくつかのグループに分類します。この「質問」と「枝分かれのルール」をデータから自動的に学習・構築することが、決定木モデルの特徴です💡
★メリット
・分かりやすい: モデルの構造が視覚的に理解しやすく、なぜそのような予測/分類になったのかが直感的に分かります。
・準備が比較的簡単: データを特別な形に変換する必要があまりありません。
★デメリット
・過学習しやすい: 学習データに過剰に適合してしまい、新しいデータに対する予測精度が悪くなることがあります(木の枝葉が細かくなりすぎるイメージ)。
2. 使用パッケージとデータ
今回は、Pima.trデータセット(MASSというRのパッケージに含まれる)を使用します。このデータセットは、アメリカ女性(21歳以上)における糖尿病の有無と健康診断データです。
※このデータセットは以下の記事でも使用しています。

妊娠回数や血糖値、BMIといった健康診断の測定値から、その人が糖尿病かどうかを予測する決定木モデルを作ります。
npreg:妊娠回数、glu:血糖値、bp:血圧、skin:皮膚の厚さ、bmi:BMI、ped:糖尿病の家族歴(遺伝的リスク)、age:年齢、type:糖尿病の有無(Yes or No)
# mlbenchパッケージがインストールされていない場合はインストール
# install.packages("MASS")
library(MASS)
data(Pima.tr)
head(Pima.tr)
# 出力結果 # npreg glu bp skin bmi ped age type #1 5 86 68 28 30.2 0.364 24 No #2 7 195 70 33 25.1 0.163 55 Yes #3 5 77 82 41 35.8 0.156 35 No #4 0 165 76 43 47.9 0.259 26 No #5 0 107 60 25 26.4 0.133 23 No #6 5 97 76 27 35.6 0.378 52 Yes
summary(Pima.tr)
# 出力結果
# npreg glu bp skin bmi ped age
# Min. : 0.00 Min. : 56.0 Min. : 38.00 Min. : 7.00 Min. :18.20 Min. :0.0850 Min. :21.00
# 1st Qu.: 1.00 1st Qu.:100.0 1st Qu.: 64.00 1st Qu.:20.75 1st Qu.:27.57 1st Qu.:0.2535 1st Qu.:23.00
# Median : 2.00 Median :120.5 Median : 70.00 Median :29.00 Median :32.80 Median :0.3725 Median :28.00
# Mean : 3.57 Mean :124.0 Mean : 71.26 Mean :29.21 Mean :32.31 Mean :0.4608 Mean :32.11
# 3rd Qu.: 6.00 3rd Qu.:144.0 3rd Qu.: 78.00 3rd Qu.:36.00 3rd Qu.:36.50 3rd Qu.:0.6160 3rd Qu.:39.25
# Max. :14.00 Max. :199.0 Max. :110.00 Max. :99.00 Max. :47.90 Max. :2.2880 Max. :63.00
# type
# No :132
# Yes: 68
summary()の結果を見ると、このPima.trデータセットには欠損値が含まれていないことが分かります。
💡補足: 欠損値がある場合は、他の値で補完する方法(平均値代入など)や、欠損値を扱えるアルゴリズムを選択することもあります。
3. Rで決定木モデルの構築と可視化
Pima.trデータセットを使って決定木モデルを構築します。
3.1 パッケージのインストールと読み込み
必要なパッケージをインストールして読み込みます。
# パッケージがインストールされていない場合はインストール
# install.packages("rpart")
# install.packages("rpart.plot")
# install.packages("caret") # データ分割のため
# install.packages("pROC") # ROC/AUC計算のため
library(rpart)
library(rpart.plot)
library(caret)
3.2 学習データとテストデータへの分割
データの70%を学習用、30%をテスト用に分割し、学習データでモデルを作成し、テストデータでその精度を検証します。
# 乱数を固定
set.seed(123)
# データを学習用とテスト用に分割 (70%を学習データ、30%をテストデータ)
train_index_pima <- createDataPartition(Pima.tr$type, p = 0.7, list = FALSE)
train_data_pima <- Pima.tr[train_index_pima, ]
test_data_pima <- Pima.tr[-train_index_pima, ]
# 分割結果の確認
print(paste("学習データ数:", nrow(train_data_pima)))
print(paste("テストデータ数:", nrow(test_data_pima)))
# 出力結果
[1] "学習データ数: 141"
[1] "テストデータ数: 59"
3.3 決定木モデルの構築・可視化
学習データを使って決定木モデルを構築します。糖尿病の有無の変数(type)を目的変数とし、それ以外の全ての変数を説明変数として指定します。
# 決定木モデルの構築 # method = "class" は分類木を指定 tree_model_pima_tr <- rpart(type ~ ., data = train_data_pima, method = "class") # 決定木の可視化 rpart.plot(tree_model_pima_tr, extra = 106, #Yesの割合(%)二値予測は106、2つ以上の予測は104が推奨 nn = TRUE #ノード番号表示 main = "決定木")
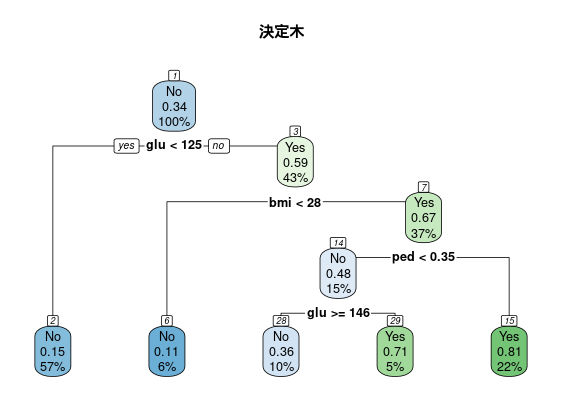 「ある人が糖尿病かどうか(Yes/No)」を、いくつかの健康診断の指標(glu:血糖値, bmi:BMI, ped:糖尿病の遺伝的リスク、など)に基づいての分類を可視化したものです。
「ある人が糖尿病かどうか(Yes/No)」を、いくつかの健康診断の指標(glu:血糖値, bmi:BMI, ped:糖尿病の遺伝的リスク、など)に基づいての分類を可視化したものです。
💡決定木の見方
箱(ノード): データの各グループを表す。(一番上のノード①(ノードの上にある番号)からスタート!)
箱の1行目(Yes/No): グループ(各ノード)の分類の結果(糖尿病の有/無=Yes/No(割合が0.5以上ならYes、未満ならNo))。
箱の2行目: グループの人のうちYes(糖尿病)である確率。
箱の3行目: 全データのうち、このグループに属する人の割合(%)。
矢印(ブランチ): 条件による枝分かれ。「yes」なら左下へ、「no」なら右下へ進む。
箱の色: 分類の結果を表しており、「No」なら青、「Yes」なら緑と判断。
💡ルールの読み解き
・ノード①の分岐質問:「血糖値(glu)は125未満ですか?」
※質問は決定木のアルゴリズムによって、よく分離できる質問として導き出されました。
答えがyesのグループは左下(ノード②)へ、noのグループは右下(ノード③)へ進みます。
ノード③のグループの人では、0.59の確率で糖尿病Yesです。ノード③に属する人の割合は、全データの43%を占めます。
・ノード③の分岐質問:「BMIは28未満ですか?」(血糖値が125以上の人に対して)
このプロセスを繰り返し、最終的に各データはいずれかの終端ノード(これ以上分岐しないノード)に分類されます。これより、決定木において「血糖値 (glucose)」や「BMI (bmi)」、「糖尿病の家族(ped)」などが糖尿病の有無を分類するのにどのように使われたかを視覚的に理解できました。
4. モデルの性能評価
作成したモデルがテストデータに対してどの程度正しく分類できるか性能を評価します。
# テストデータで予測を行う (分類クラスを予測)
predicted_tree <- predict(tree_model_pima_tr, test_data_pima, type = "class")
# 予測結果と実際の答えを元に混同行列と各種指標を計算
caret_cm_direct <- confusionMatrix(data = predicted_tree,
reference = test_data_pima$type,
positive = "Yes")
caret_cm_direct
#出力結果
#Confusion Matrix and Statistics
# Reference
#Prediction No Yes #混同行列
# No 33 9 #予測がNoの人で実際Noであった人33人、実際Yesだった人9人
# Yes 6 11 #予測がYesの人で実際Noであった人6人、実際Yesだった人11人
# Accuracy : 0.7458 #正解率
# 95% CI : (0.6156, 0.8502)
# No Information Rate : 0.661
# P-Value [Acc > NIR] : 0.1062
# Kappa : 0.4112
# Mcnemar's Test P-Value : 0.6056
# Sensitivity : 0.5500 #再現率
# Specificity : 0.8462 #特異度
# Pos Pred Value : 0.6471 #適合率
# Neg Pred Value : 0.7857
# Prevalence : 0.3390
# Detection Rate : 0.1864
# Detection Prevalence : 0.2881
# Balanced Accuracy : 0.6981
# 'Positive' Class : Yes
このモデルの全体的な正解率は約74.6%ですが、例えば実際に糖尿病である人の半分近くを糖尿病ではないと予測しており、モデルの良し悪しを判断するには充分な議論が必要と考えられます。
今回の記事では、決定木モデルを作成し、基本的な性能評価を行いました。
5. まとめ
今回は、機械学習の基本的な手法である決定木について、Pima.trデータセットを例に、その考え方からRのrpartパッケージを使ったモデル構築、可視化、そして簡単な評価までの一連の流れを解説しました。
決定木は、そのシンプルさと解釈のしやすさから、多くの場面で活用される機械学習の手法です。より複雑なモデルを学ぶ上での基礎にもなりますので、ぜひこの機会に実際にコードを動かしてみてください。






コメント